পাইথনে একটি বাইনারি গাছে দুটি নোডের মধ্যে দূরত্ব খুঁজে বের করার জন্য প্রোগ্রাম

ধরুন, আমাদের একটি বাইনারি ট্রি দেওয়া হয়েছে এবং বাইনারি গাছের দুটি নোডের মধ্যে দূরত্ব খুঁজে বের করতে বলা হয়েছে। আমরা একটি গ্রাফের মতো দুটি নোডের মধ্যে প্রান্তগুলি খুঁজে বের করি এবং প্রান্তের সংখ্যা বা তাদের মধ্যে দূরত্ব প্রদান করি। একটি গাছের একটি নোডের গঠন নিচের মত রয়েছে -

data : <integer value>
right : <pointer to another node of the tree>
left : <pointer to another node of the tree>

সুতরাং, যদি ইনপুট মত হয়

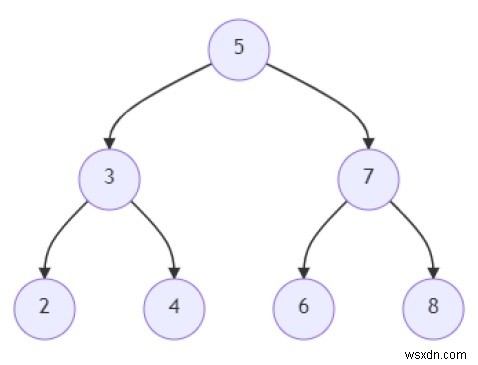
এবং যে নোডগুলির মধ্যে আমাদের দূরত্ব খুঁজে বের করতে হবে তা হল 2 এবং 8; তাহলে আউটপুট হবে 4.

দুটি নোড 2 এবং 8 এর মধ্যে প্রান্তগুলি হল:(2, 3), (3, 5), (5, 7), এবং (7, 8)। তাদের মধ্যে পথের মধ্যে 4টি প্রান্ত রয়েছে, তাই দূরত্ব হল 4৷

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• একটি ফাংশন findLca() সংজ্ঞায়িত করুন। এটি root, p, q
  নেবে
  • যদি রুট নাল এর মত হয়, তাহলে
    • রিটার্ন নাল
  • মূলের ডেটা যদি (p,q) এর যেকোনো একটি হয়, তাহলে
    • রিটার্ন রুট
  • বামে :=findLca(মূলের বামে, p, q)
  • ডান:=findLca(মূলের ডান, p, q)
  • যদি বাম এবং ডান শূন্য না হয়, তাহলে
    • রিটার্ন রুট
  • বাম বা ডানে ফিরুন
• একটি ফাংশন সংজ্ঞায়িত করুন findDist()। এটি রুট, ডেটা
  নেবে
  • সারি :=একটি নতুন ডিক
  • সারির শেষে একটি নতুন জোড়া (রুট, 0) ঢোকান
  • যখন সারি খালি না থাকে, কর
    • বর্তমান :=সারিতে থাকা বামতম জোড়ার প্রথম মান
    • dist :=সারিতে থাকা বামতম জোড়ার দ্বিতীয় মান
    • যদি বর্তমানের ডেটা ডেটার মতো হয়, তাহলে
      • প্রত্যাবর্তন জেলা
    • কারেন্টের বাম অংশ যদি শূন্য না হয়, তাহলে
      • সারিতে জোড়া (বর্তমানের বামে, dist+1) যোগ করুন
    • যদি কারেন্টের ডানদিকে শূন্য না হয়, তাহলে
      • সারিতে জোড়া (current.right, dist+1) যোগ করুন
• নোড :=findLca(root, p, q)
• রিটার্ন FindDist(node, p) + findDist(node, q)

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

import collections
class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.data = data
      self.left = left
      self.right = right

def insert(temp,data):
   que = []
   que.append(temp)
   while (len(que)):
      temp = que[0]
      que.pop(0)
      if (not temp.left):
         if data is not None:
            temp.left = TreeNode(data)
         else:
            temp.left = TreeNode(0)
         break
      else:
         que.append(temp.left)

      if (not temp.right):
         if data is not None:
            temp.right = TreeNode(data)
         else:
            temp.right = TreeNode(0)
         break
      else:
         que.append(temp.right)

def make_tree(elements):
   Tree = TreeNode(elements[0])
   for element in elements[1:]:
      insert(Tree, element)
   return Tree

def search_node(root, element):
   if (root == None):
      return None

   if (root.data == element):
      return root

   res1 = search_node(root.left, element)
   if res1:
      return res1

   res2 = search_node(root.right, element)
   return res2

def print_tree(root):
   if root is not None:
      print_tree(root.left)
      print(root.data, end == ', ')
      print_tree(root.right)

def findLca(root, p, q):
   if root is None:
      return None
   if root.data in (p,q):
      return root
   left = findLca(root.left, p, q)
   right = findLca(root.right, p, q)
   if left and right:
      return root
   return left or right

def findDist(root, data):
   queue = collections.deque()
   queue.append((root, 0))
   while queue:
      current, dist = queue.popleft()
      if current.data == data:
         return dist
      if current.left: queue.append((current.left, dist+1))
      if current.right: queue.append((current.right, dist+1))

def solve(root, p, q):
   node = findLca(root, p, q)
   return findDist(node, p) + findDist(node, q)

root = make_tree([5, 3, 7, 2, 4, 6, 8])
print(solve(root, 2, 8))

ইনপুট

root = make_tree([5, 3, 7, 2, 4, 6, 8])
print(solve(root, 2, 8))

আউটপুট

4