আমাদের একটি সমদ্বিবাহু ত্রিভুজ দেওয়া হয়েছে। সমদ্বিবাহু ত্রিভুজ হল একটি যার দুটি বাহু সমান দৈর্ঘ্যের। সমকোণী ত্রিভুজ হল যেটির উচ্চতা (ডুমুরে ag) এবং ভিত্তি (ডুমুরে dg) একে অপরের সাথে লম্ব। লক্ষ্য হল সর্বাধিক সংখ্যক বর্গক্ষেত্র খুঁজে বের করা যা এই ডান সমদ্বিবাহু ত্রিভুজ 2 বর্গ এককের মধ্যে ফিট করতে পারে। পাশের বেস বা উচ্চতা (উভয় সমান) ইনপুট হিসাবে নেওয়া হয়। বর্গের সংখ্যা আউটপুট।
সমস্যাটি বুঝতে নিচের চিত্রটি পড়ুন
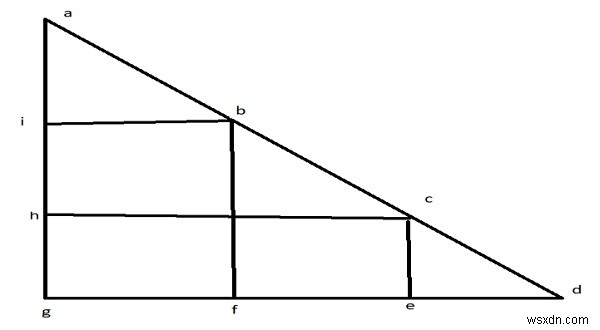
উচ্চতা ag এবং ভিত্তি gd এর প্রদত্ত ত্রিভুজটির প্রতিটি বাহুর 2টির 3টি বর্গ রয়েছে। কোণার প্রান্ত থেকে 'a' এবং 'd', ত্রিভুজ aib এবং cde কখনই কোনো বর্গক্ষেত্রে অবদান রাখবে না। তাই প্রথমে আমাদের এই ত্রিভুজের জন্য দৈর্ঘ্যের অতিরিক্ত 2 ইউনিট প্রয়োজন হবে। না, সংখ্যা গণনা করতে আমাদের অবশিষ্ট বেস gd(বা উচ্চতা ag) কে 2 দ্বারা ভাগ করতে হবে। বর্গক্ষেত্র উচ্চতা ( ag) এর ক্ষেত্রেও তাই হবে।
যখন(বেস> 2) স্কোয়ার+=(বেস-2)/2 বেস =বেস-2। Ap =b*(b+1)/2 এর সূত্র ব্যবহার করুন….যেখানে নতুন b=b-2
উদাহরণ দিয়ে বোঝা যাক।
ইনপুট − ভিত্তি:12
আউটপুট − বর্গের সংখ্যা :15
ব্যাখ্যা
বেস 12>2, বর্গ 10/2=5, নতুন বেস 12-2=10বেস 10>2, বর্গ 8/2=4, নতুন বেস 10-2=8বেস 8>2, বর্গ 6/2=3 , নতুন বেস 8-2=6বেস 6>2, বর্গ 4/2=2, নতুন বেস 6-2=4বেস 4>2, বর্গ 2/2=1, নতুন বেস 4-2=2বেস 2>2 X মোট বর্গক্ষেত্র =5+4+3+2+1=15
ইনপুট − .5
আউটপুট − বর্গের গণনা − 1
ব্যাখ্যা
বেস 5>2, বর্গ 3/2=1, নতুন বেস 5-2=3বেস 3>2, বর্গ 1/2=0, নতুন বেস 3-2=1বেস 1>2 X মোট বর্গক্ষেত্র=1
নিম্নলিখিত প্রোগ্রামে ব্যবহৃত পদ্ধতি
-
পূর্ণসংখ্যা পরিবর্তনশীল বেস ত্রিভুজের ভিত্তি সংরক্ষণ করতে ব্যবহৃত হয়..
-
ফাংশন numofSquares(int b) ব্যবহার করা হয় বর্গের সংখ্যা গণনা করতে যেগুলি বেস b সহ ত্রিভুজ মিটমাট করতে পারে।
-
প্রথমে b=b-2 -কোণার প্রান্ত থেকে অতিরিক্ত স্থান
-
সূত্র অনুসারে, b=floor(b/2), এই নতুন b এর b*(b+1)/2 পাশের 2 বর্গ থাকতে পারে।
-
বর্গ সংখ্যা হিসাবে গণনা ফেরত দিন।
উদাহরণ
#include#include int numofSquares(int b){ // অতিরিক্ত অংশ অপসারণ করা আমাদের // সর্বদা b =(b - 2) প্রয়োজন হবে; // যেহেতু প্রতিটি বর্গক্ষেত্রের বেস // দৈর্ঘ্য 2 b =তল (b / 2); রিটার্ন b * (b + 1)/2;}int main(){ int base =8; printf("সর্বোচ্চ বর্গক্ষেত্রের সংখ্যা যা মিটমাট করা যায় :%d", numofSquares(বেস)); রিটার্ন 0;
আউটপুট
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট −
উৎপন্ন করবে <পূর্ব>সর্বোচ্চ নম্বর বর্গাকারের যা মিটমাট করা যায় :6

