প্রদত্ত কাজটি হল 'a' সহ সর্বাধিক সংখ্যক বর্গক্ষেত্র খুঁজে বের করা যা 's' এর বেস সহ একটি গিভরাইট কোণ সমদ্বিবাহু ত্রিভুজের মধ্যে ফিট করতে পারে (একটি সমদ্বিবাহু ত্রিভুজের কমপক্ষে 2টি সমান বাহু রয়েছে)।
আসুন এখন বুঝি একটি উদাহরণ ব্যবহার করে আমাদের কী করতে হবে:
ইনপুট
s=5, a=1
আউটপুট
10
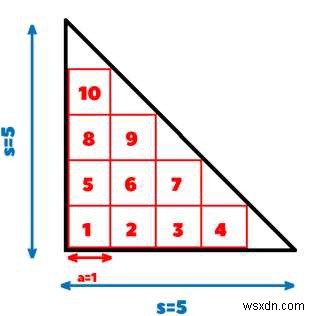
ব্যাখ্যা − s কে a দ্বারা ভাগ করে এবং 1 বিয়োগ করে বেসের বর্গক্ষেত্রের সংখ্যা গণনা করা যেতে পারে। সুতরাং বেসে বর্গ সংখ্যা =5/1 – 1 =4।
একইভাবে যখন নীচের 4টি বর্গক্ষেত্র স্থাপন করা হয় তখন আমরা ভিত্তি(s-a) সহ একটি নতুন সমদ্বিবাহু ত্রিভুজ পাই এবং তারপরে আমরা একই পদ্ধতিটি পুনরাবৃত্তি করি এবং 3টি বর্গক্ষেত্র পেতে পারি যতক্ষণ না উপরে একটি একক বর্গক্ষেত্র স্থাপন করা হয়।
ইনপুট
s=7, a=2
আউটপুট
3
নিম্নলিখিত প্রোগ্রামে ব্যবহৃত পদ্ধতি
-
সর্বাধিক সংখ্যক বর্গ বের করতে আমাদের ত্রিভুজের ভিত্তি থেকে শুরু করতে হবে এবং বর্গ সংখ্যা বের করতে হবে।
-
বর্গক্ষেত্রের সংখ্যা বের করতে আমরা স্কোয়ারের পাশে ভিত্তি s কে ভাগ করব এবং এর থেকে 1 বিয়োগ করব =s/a – 1।
-
তারপর এটি আমাদেরকে বেস (s - a) সহ আরেকটি সমদ্বিবাহু ত্রিভুজ ছেড়ে দেবে যা এটির নীচে পূর্ববর্তী সারির চেয়ে একটি কম বর্গক্ষেত্র মিটমাট করবে যা আমরা নিম্নলিখিত উপায়ে গণনা করতে পারি −
পরবর্তী সারিতে বর্গক্ষেত্র =(s - a)/a – 1 =(s/a – a/a) – 1=s/a - 1 - 1 =s/a – 2 =পূর্ববর্তী সারির চেয়ে এক বর্গ কম৷
-
বর্গক্ষেত্রের সংখ্যা কমতে থাকে যতক্ষণ না এটি 1 এ পৌঁছায়, তাই আমাদের শুধুমাত্র বেস সারিতে বর্গ সংখ্যা খুঁজে বের করতে হবে এবং চূড়ান্ত যোগফল খুঁজে পেতে প্রাকৃতিক সংখ্যা যোগ করার সূত্র ব্যবহার করতে হবে −
(n) * (n + 1) / 2
এই ক্ষেত্রে সূত্রটি হয়ে যায় −(s/a)-1) * (s/a) / 2
উদাহরণ
#include<bits/stdc++.h>
using namespace std;
int Max(int s, int a){
//formula for calculating maximum squares
return ((s / a) - 1) * (s / a) / 2;
}
//Main function
int main(){
int s = 5, a = 1;
cout <<"Maximum squares possible are: "<<Max(s,a);
return 0;
} আউটপুট
10


