একটি গ্রাফের ইনসিডেন্স ম্যাট্রিক্স হল মেমরিতে সংরক্ষণ করার জন্য একটি গ্রাফের আরেকটি উপস্থাপনা। এই ম্যাট্রিক্স একটি বর্গ ম্যাট্রিক্স নয়। ইনসিডেন্স ম্যাট্রিক্সের ক্রম হল V x E। যেখানে V হল শীর্ষবিন্দুর সংখ্যা এবং E হল গ্রাফের প্রান্তের সংখ্যা।
এই ম্যাট্রিক্সের প্রতিটি সারিতে আমরা শীর্ষবিন্দু স্থাপন করছি, এবং প্রতিটি কলামে প্রান্তগুলি স্থাপন করা হয়েছে। একটি প্রান্ত e {u, v}-এর জন্য এই উপস্থাপনায়, এটি কলাম e-এর u এবং v স্থানের জন্য 1 দ্বারা চিহ্নিত করা হবে।
অ্যাডজাসেন্সি ম্যাট্রিক্স প্রতিনিধিত্বের জটিলতা
-
ইনসিডেন্স ম্যাট্রিক্স উপস্থাপনাটি গণনা করার সময় O(Vx E) পরিমাণ স্থান নেয়। সম্পূর্ণ গ্রাফের জন্য প্রান্তের সংখ্যা হবে V(V-1)/2। তাই ইনসিডেন্স ম্যাট্রিক্স মেমরিতে বড় জায়গা নেয়।
ইনপুট
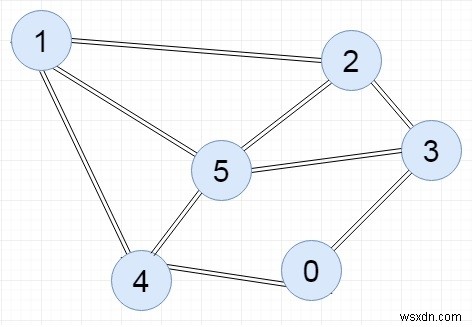
আউটপুট
| | E0 | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 3 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
অ্যালগরিদম
add_edge(u, v)
ইনপুট − একটি প্রান্তের u এবং v {u,v}
আউটপুট − গ্রাফ G
এর ইনসিডেন্স ম্যাট্রিক্সপ্রথমে, ঘটনা ম্যাট্রিক্সের জন্য প্রান্তের সংখ্যা ed_cnt হল 0।
Begin ed_cnt := ed_cnt + 1 inc_matrix[u, ed_cnt] := 1 inc_matrix[v, ed_cnt] := 1 End
উদাহরণ কোড (C++)
#include<iostream>
using namespace std;
int inc_arr[20][20]; //initial array to hold incidence matrix
int ed_no = 0;
void displayMatrix(int v, int e) {
int i, j;
for(i = 0; i < v; i++) {
for(j = 0; j < e; j++) {
cout << inc_arr[i][j] << " ";
}
cout << endl;
}
}
void add_edge(int u, int v) { //function to add edge into the matrix with edge number
inc_arr[u][ed_no] = 1;
inc_arr[v][ed_no] = 1;
ed_no++; //increase the edge number
}
main(int argc, char* argv[]) {
int v = 6; //there are 6 vertices in the graph
int e = 9; //there are 9 edges in the graph
add_edge(0, 4);
add_edge(0, 3);
add_edge(1, 2);
add_edge(1, 4);
add_edge(1, 5);
add_edge(2, 3);
add_edge(2, 5);
add_edge(5, 3);
add_edge(5, 4);
displayMatrix(v, e);
} আউটপুট
1 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 1 0 1 0 1 0 0 1 0 0 0 0 1 0 0 0 0 1 0 1 1 1


