একটি গ্রাফের সংলগ্ন ম্যাট্রিক্স হল V x V আকারের একটি বর্গ ম্যাট্রিক্স। V হল G গ্রাফের শীর্ষবিন্দুর সংখ্যা। এই ম্যাট্রিক্সে প্রতিটি পাশে V শীর্ষবিন্দু চিহ্নিত করা হয়েছে। যদি গ্রাফটিতে i থেকে j শীর্ষবিন্দুর কিছু প্রান্ত থাকে, তাহলে i th এ সংলগ্ন ম্যাট্রিক্সে সারি এবং j th কলাম এটি হবে 1 (বা ওজনযুক্ত গ্রাফের জন্য কিছু অ-শূন্য মান), অন্যথায় সেই স্থানটি 0 হবে।
অ্যাডজাসেন্সি ম্যাট্রিক্স উপস্থাপনার জটিলতা:
-
সংলগ্ন ম্যাট্রিক্স উপস্থাপনাটি গণনা করার সময় O(V2) পরিমাণ স্থান নেয়। গ্রাফে যখন সর্বোচ্চ সংখ্যক প্রান্ত এবং ন্যূনতম সংখ্যক প্রান্ত থাকে, উভয় ক্ষেত্রেই প্রয়োজনীয় স্থান একই হবে৷
ইনপুট:
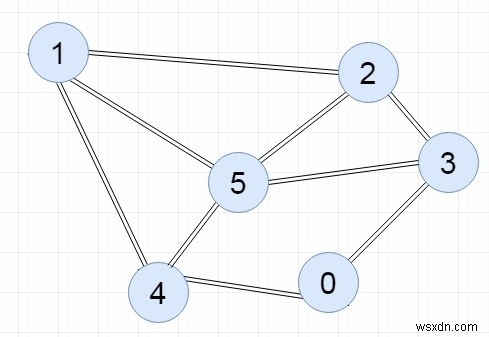
আউটপুট:
| | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 0 | 1 | 0 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 | 0 | 1 |
| 5 | 0 | 1 | 1 | 1 | 1 | 0 |
অ্যালগরিদম
add_edge(u, v)
ইনপুট৷ :একটি প্রান্তের u এবং v {u,v}
আউটপুট৷ :G
গ্রাফের সংলগ্নতা ম্যাট্রিক্সBegin adj_matrix[u, v] := 1 adj_matrix[v, u] := 1 End
উদাহরণ কোড
#include<iostream>
using namespace std;
int vertArr[20][20]; //the adjacency matrix initially 0
int count = 0;
void displayMatrix(int v) {
int i, j;
for(i = 0; i < v; i++) {
for(j = 0; j < v; j++) {
cout << vertArr[i][j] << " ";
}
cout << endl;
}
}
void add_edge(int u, int v) { //function to add edge into the matrix
vertArr[u][v] = 1;
vertArr[v][u] = 1;
}
main(int argc, char* argv[]) {
int v = 6; //there are 6 vertices in the graph
add_edge(0, 4);
add_edge(0, 3);
add_edge(1, 2);
add_edge(1, 4);
add_edge(1, 5);
add_edge(2, 3);
add_edge(2, 5);
add_edge(5, 3);
add_edge(5, 4);
displayMatrix(v);
} আউটপুট
0 0 0 1 1 0 0 0 1 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 1 0 0 0 1 0 1 1 1 1 0


