প্রদত্ত গ্রাফটি C++ প্রোগ্রামে DFS ব্যবহার করে দ্বিপক্ষীয় কিনা তা পরীক্ষা করুন

ধরুন আমাদের একটি সংযুক্ত গ্রাফ আছে; আমাদের গ্রাফটি দ্বিপক্ষীয় কিনা তা পরীক্ষা করতে হবে। যদি গ্রাফ রঙ করা সম্ভব হয় তবে দুটি রঙ প্রয়োগ করা হয় যাতে একটি সেটের নোডগুলি একই রঙে রঙিন হয়।

সুতরাং, যদি ইনপুট মত হয়

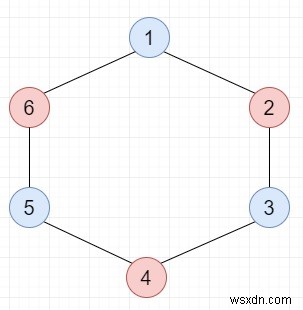
তাহলে আউটপুট হবে True

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

একটি ফাংশন সংজ্ঞায়িত করুন insert_edge(), এটি একটি প্রান্ত অ্যারে adj, u, v,
adj[u] এর শেষে v ঢোকান
adj[v] এর শেষে u ঢোকান
প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন,
adj[v] এ প্রতিটি u এর জন্য, কর
- যদি পরিদর্শন করা হয় [u] মিথ্যার মত হয়, তাহলে −
  - পরিদর্শন করেছেন[u] :=সত্য
  - রঙ[u] :=রঙের উল্টো [v]
  - যদি না হয়_bipartite_graph(adj, u, visited, color), তাহলে −
    - মিথ্যে ফেরত দিন
- অন্যথায় যখন রঙ[u] রঙ[v] এর মত হয়, তাহলে −
  - মিথ্যে ফেরত দিন
সত্য ফেরত দিন

উদাহরণ (C++)

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

#include <bits/stdc++.h>
using namespace std;
void insert_edge(vector<int> adj[], int u, int v){
   adj[u].push_back(v);
   adj[v].push_back(u);
}
bool is_bipartite_graph(vector<int> adj[], int v, vector<bool>& visited, vector<int>& color){
   for (int u : adj[v]) {
      if (visited[u] == false) {
         visited[u] = true;
         color[u] = !color[v];
         if (!is_bipartite_graph(adj, u, visited, color))
            return false;
      }
      else if (color[u] == color[v])
      return false;
   }
   return true;
}
int main() {
   int N = 6;
   vector<int> adj_list[N + 1];
   vector<bool> visited(N + 1);
   vector<int> color(N + 1);
   insert_edge(adj_list, 1, 2);
   insert_edge(adj_list, 2, 3);
   insert_edge(adj_list, 3, 4);
   insert_edge(adj_list, 4, 5);
   insert_edge(adj_list, 5, 6);
   insert_edge(adj_list, 6, 1);
   visited[1] = true;
   color[1] = 0;
   cout << (is_bipartite_graph(adj_list, 1, visited, color));
}

ইনপুট

insert_edge(adj_list, 1, 2);
insert_edge(adj_list, 2, 3);
insert_edge(adj_list, 3, 4);
insert_edge(adj_list, 4, 5);
insert_edge(adj_list, 5, 6);
insert_edge(adj_list, 6, 1);