প্রদত্ত গ্রাফটি পাইথনে দ্বিপক্ষীয় কি না তা পরীক্ষা করার জন্য প্রোগ্রাম

ধরুন আমাদের একটি অনির্দেশিত গ্রাফ আছে, আমাদের গ্রাফটি দ্বিপক্ষীয় কিনা তা পরীক্ষা করতে হবে। যেহেতু আমরা জানি একটি গ্রাফ দ্বিপক্ষীয় হয় যখন আমরা গ্রাফের নোডগুলিকে দুটি সেট A এবং B এ বিভক্ত করতে পারি যাতে গ্রাফের প্রতিটি প্রান্ত {u,v} এ একটি নোড u A তে এবং আরেকটি নোড v B তে থাকে।

সুতরাং, যদি ইনপুট মত হয়

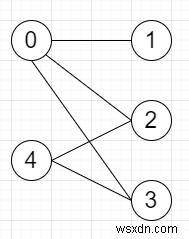
তাহলে আউটপুট হবে True, [0,4] সেট A এ আছে এবং [1,2,3] সেট B এ আছে এবং সমস্ত প্রান্ত A থেকে B বা B থেকে A, A থেকে A বা B থেকে B নয় .

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব−

• একটি ফাংশন dfs() সংজ্ঞায়িত করুন। এটি উৎস গ্রহণ করবে

• গ্রাফের প্রতিটি শীর্ষবিন্দুর জন্য [উৎস], করুন

  • যদি রঙ [ভার্টেক্স] -1 এর মত না হয়, তাহলে

    • যদি রঙ[ভার্টেক্স] রঙের [উৎস] হিসাবে একই হয়, তাহলে

      • ফলাফল[0] :=মিথ্যা

      • ফেরত

    • পরবর্তী পুনরাবৃত্তির জন্য যান

  • রঙ[ভার্টেক্স] :=1 - রঙ[উৎস]

  • dfs(vertex)

• প্রধান পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন−

• n :=arr এর আকার

• গ্রাফ :=শীর্ষবিন্দু 0 থেকে n-1

  এর জন্য খালি সংলগ্ন তালিকা

• 0 থেকে n রেঞ্জের জন্য, করুন

  • প্রতিটি j এর জন্য arr[i], do

    • গ্রাফ[j]

      -এ ঢোকান

    • গ্রাফ[i]

      -এ j সন্নিবেশ করান

  • রঙ :=n আকারের একটি তালিকা এবং -1

    দিয়ে পূরণ করুন

  • ফলাফল :=একটি সত্য মান সহ একটি তালিকা

• 0 থেকে n রেঞ্জের জন্য, করুন

  • যদি রঙ[i] -1 এর মত হয়, তাহলে

  • dfs(i)

• রিটার্ন ফলাফল[0]

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

from collections import defaultdict
class Solution:
   def solve(self, arr):
      n = len(arr)
      graph = [set() for i in range(n)]
      for i in range(n):
         for j in arr[i]:
            graph[j].add(i)
            graph[i].add(j)
      color = [-1] * n
      result = [True]
      def dfs(source):
      for child in graph[source]:
         if color[child] != -1:
            if color[child] == color[source]:
               result[0] = False
               return
            continue
      color[child] = 1 - color[source]
      dfs(child)
   for i in range(n):
      if color[i] == -1:
      dfs(i)
   return result[0]
ob = Solution()
graph = [[1,2,3],[0],[0,4],[0,4],[2,3]]
print(ob.solve(graph))

ইনপুট

graph = [[1,2,3],[0],[0,4],[0,4],[2,3]]

আউটপুট

True