বিবেচনা করুন আমাদের কয়েকটি নোড সহ একটি বাইনারি ট্রি আছে৷ আমাদের u এবং v দুটি নোডের মধ্যে দূরত্ব খুঁজে বের করতে হবে। ধরুন গাছটি নিচের মত −
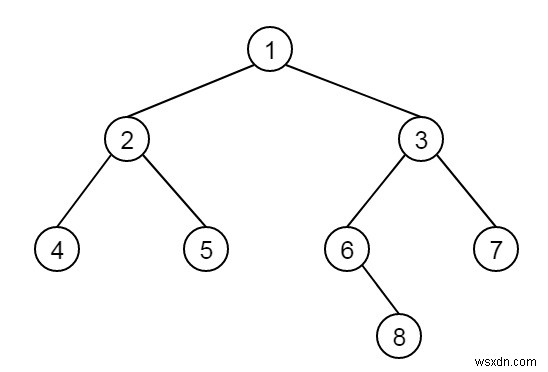
এখন (4, 6) =4 এর মধ্যে দূরত্ব, পথের দৈর্ঘ্য 4, (5, 8) =5 ইত্যাদির মধ্যে দৈর্ঘ্য।
এই সমস্যাটি সমাধান করার জন্য, আমরা LCA (সর্বনিম্ন সাধারণ পূর্বপুরুষ) খুঁজে পাব, তারপর LCA থেকে দুটি নোডের দূরত্ব গণনা করব।
উদাহরণ
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
};
Node* getNode(int data) {
Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return node;
}
Node* LowestCommonAncestor(Node * root, int n1,int n2) {
if (root == NULL)
return root;
if (root->data == n1 || root->data == n2)
return root;
Node* left = LowestCommonAncestor(root->left, n1, n2);
Node* right = LowestCommonAncestor(root->right, n1, n2);
if (left != NULL && right != NULL)
return root;
if (left != NULL)
return LowestCommonAncestor(root->left, n1, n2);
return LowestCommonAncestor(root->right, n1, n2);
}
int getLevel(Node *root, int k, int level) {
if(root == NULL) return -1;
if(root->data == k) return level;
int left = getLevel(root->left, k, level+1);
if (left == -1)
return getLevel(root->right, k, level+1);
return left;
}
int findDistance(Node* root, int a, int b) {
Node* lca = LowestCommonAncestor(root, a , b);
int dist1 = getLevel(lca, a, 0);
int dist2 = getLevel(lca, b, 0);
return dist1 + dist2;
}
int main() {
Node* root = getNode(1);
root->left = getNode(2);
root->right = getNode(3);
root->left->left = getNode(4);
root->left->right = getNode(5);
root->right->left = getNode(6);
root->right->right = getNode(7);
root->right->left->right = getNode(8);
cout << "Distance between (4, 6) is: " << findDistance(root, 4, 6);
cout << "\nDistance between (8, 5) is: " << findDistance(root, 8, 5);
} আউটপুট
Distance between (4, 6) is: 4 Distance between (8, 5) is: 5


