এই সমস্যায়, আমাদের একটি বাইনারি ট্রি এবং একটি পূর্ণসংখ্যা K দেওয়া হয়েছে এবং আমাদেরকে বাইনারি গাছের সমস্ত নোড প্রিন্ট করতে হবে যেগুলির চাইল্ড সাবট্রিতে K পাতা রয়েছে৷
বাইনারী গাছ একটি বিশেষ গাছ যার প্রতিটি নোডে সর্বোচ্চ দুটি নোড থাকে (এক/দুই/কোনটি নয়)।
লিফ নোড একটি বাইনারি গাছ হল গাছের শেষে নোড।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক -
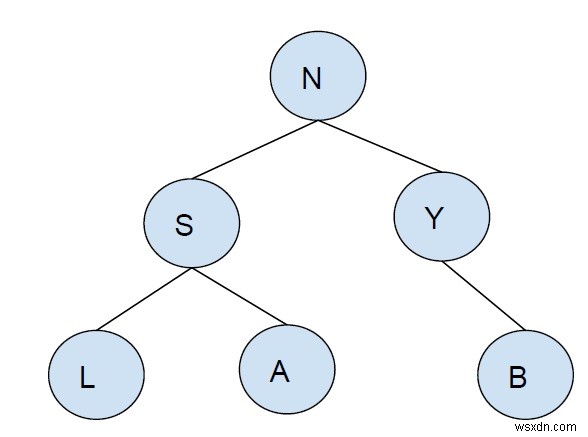
কে =2
আউটপুট - {S}
এই সমস্যা সমাধানের জন্য, আমরা গাছের জন্য ট্রাভার্সাল (পোস্টডার) করব। এখন, পাতার যোগফল K হলে আমরা প্রতিটি বাম সাবট্রি এবং ডান সাবট্রি দেখতে পাব, কারেন্ট নোড প্রিন্ট করুন। অন্যথায় পুনরাবৃত্তভাবে কল করুন, সাবট্রির পাতা গণনা করুন।
এই সমাধানটি ট্রাভার্সিং এর উপর ভিত্তি করে তাই জটিলতা গাছের আকারের ক্রম অনুসারে হবে। সময় জটিলতা − O(n)
উদাহরণ
উপরোক্ত পদ্ধতি বাস্তবায়নের জন্য প্রোগ্রাম
#include<bits/stdc++.h>
using namespace std;
struct Node{
char data ;
struct Node * left, * right ;
};
struct Node * insertNode(char data){
struct Node * node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
int nodeWithKLeave(struct Node *ptr,int k){
if (ptr == NULL)
return 0;
if (ptr->left == NULL && ptr->right == NULL)
return 1;
int total = nodeWithKLeave(ptr->left, k) + nodeWithKLeave(ptr->right, k);
if (k == total)
cout<<ptr->data<<" ";
return total;
}
int main() {
struct Node *root = insertNode('A');
root->left = insertNode('B');
root->right = insertNode('K');
root->left->left = insertNode('N');
root->left->right = insertNode('S');
root->left->left->left = insertNode('X');
root->left->left->right = insertNode('H');
root->right->right = insertNode('E');
root->right->left = insertNode('T');
root->right->left->left = insertNode('O');
root->right->left->right = insertNode('P');
int K = 2;
cout<<"Nodes with "<<K<<" leaves is :\n";
nodeWithKLeave(root, K);
return 0;
} আউটপুট
Nodes with 2 leaves are: N T


