সংকুচিত কোয়াডট্রিস
একটি উপবিভক্ত কক্ষের সাথে সম্পর্কিত প্রতিটি নোড সংরক্ষণ করার সময়, আমরা অনেক খালি নোড সংরক্ষণ করতে পারি। এই ধরনের বিরল গাছের আকার কমানো সম্ভব শুধুমাত্র এমন উপবৃক্ষ সংরক্ষণ করে যার পাতায় আকর্ষণীয় তথ্য রয়েছে (যেমন "গুরুত্বপূর্ণ উপবৃক্ষ")। আবার আমরা প্রকৃতপক্ষে আকার আরও আরও কমাতে পারি। যখন আমরা শুধুমাত্র গুরুত্বপূর্ণ উপবৃক্ষগুলি বিবেচনা করি, তখন ছাঁটাই প্রক্রিয়া গাছের দীর্ঘ পথ এড়াতে পারে যেখানে মধ্যবর্তী নোডের দুটি ডিগ্রি রয়েছে (একটি পিতামাতা এবং একটি সন্তানের সাথে একটি লিঙ্ক)। দেখা যাচ্ছে যে আমাদের শুধুমাত্র এই পথের শুরুতে নোড U সংরক্ষণ করতে হবে (এবং মুছে ফেলা নোডগুলিকে উপস্থাপন করার জন্য এটির সাথে কিছু মেটা-ডেটা যুক্ত করতে হবে) এবং এর শেষে উপবৃক্ষটিকে U-তে সংযুক্ত করতে হবে। এই সংকুচিত গাছগুলিতে এখনও একটি রৈখিক উচ্চতা যখন "খারাপ" ইনপুট পয়েন্ট দেওয়া হয়।
যদিও আমরা এই সংকোচনটি সম্পাদন করার সময় অনেক গাছ কেটে ফেলি, তবুও Z-অর্ডার কার্ভের সুবিধা নিয়ে লগারিদমিক-টাইম সন্নিবেশ, মুছে ফেলা এবং অনুসন্ধান করা সম্ভব। Z-অর্ডার বক্ররেখা O(1) সময়ে পূর্ণ কোয়াডট্রির প্রতিটি কোষকে (এবং এমনকি সংকুচিত কোয়াডট্রিকে) একটি 1-মাত্রিক রেখায় রূপান্তরিত করে (এবং O(1) সময়েও এটিকে আবার রূপান্তরিত করে), একটি মোট অর্ডার তৈরি করে উপাদানের উপর। এখন, আমরা অর্ডারকৃত সেটগুলির জন্য একটি ডেটা স্ট্রাকচারে কোয়াডট্রি সংরক্ষণ করতে সক্ষম হতে পারি (যেটিতে আমরা গাছের নোডগুলি সংরক্ষণ করি)। এখন, চালিয়ে যাওয়ার আগে আমাদের অবশ্যই একটি যুক্তিসঙ্গত অনুমান জানাতে হবে:আমরা ধরে নিই যে দুটি বাস্তব সংখ্যা α,β € [0,1] বাইনারি হিসাবে চিহ্নিত করা হয়েছে, আমরা O(1) সময়ে গণনা করতে পারি প্রথম বিটের সূচকটি যেখানে তারা ভিন্ন আমরা আরও অনুমান করি যে আমরা O(1) সময়ে কোয়াডট্রিতে দুটি বিন্দু/কোষের ক্ষুদ্রতম সাধারণ পূর্বপুরুষ গণনা করতে পারি এবং তাদের আপেক্ষিক Z-ক্রম স্থাপন করতে পারি এবং আমরা O(1) সময়ে ফ্লোর ফাংশন গণনা করতে পারি। এই অনুমানগুলির সাথে, একটি প্রদত্ত বিন্দু Q এর বিন্দুর অবস্থান (অর্থাৎ Q ধারণ করে এমন ঘরটি সন্ধান করুন), মুছে ফেলা এবং সন্নিবেশের ক্রিয়াকলাপগুলি সমস্ত O(n log n) সময়ে (অর্থাৎ একটি অনুসন্ধান করতে যে সময় লাগে) সঞ্চালিত হতে পারে অন্তর্নিহিত অর্ডার সেট ডেটা স্ট্রাকচার)।
Q-এর জন্য একটি বিন্দু অবস্থান সম্পাদন করতে (অর্থাৎ সংকুচিত গাছে এর ঘর নির্ধারণ করা)
- বিদ্যমান সেলটি সংকুচিত ট্রিতে পাওয়া যায় যা Z-ক্রমের Q-এর আগে আসে। এই সেল V. কল করুন
- যদি Q€V সঞ্চালিত হয়, V ফেরত দিন।
- অন্যথায়, একটি সংকুচিত চতুর্গাছের মধ্যে Q বিন্দু এবং কোষ V-এর ক্ষুদ্রতম সাধারণ পূর্বপুরুষ কী হত তা খুঁজুন। এই পূর্বপুরুষ কোষটিকে U. বলুন
- জেড-অর্ডারে U-এর আগে আসা সংকুচিত ট্রিতে বিদ্যমান ঘরটি খুঁজুন এবং এটি ফেরত দিন।
সুনির্দিষ্ট বিবরণে না গিয়ে, সন্নিবেশ এবং মুছে ফেলার জন্য আমরা প্রথমে যে জিনিসটি সন্নিবেশ/মুছে দিতে চাই তার জন্য একটি পয়েন্ট অবস্থান করি এবং তারপর এটি সন্নিবেশ/মুছে ফেলি। গাছটিকে যথাযথভাবে পুনর্নির্মাণ করার জন্য যত্ন নেওয়া উচিত, প্রয়োজন অনুসারে নোড তৈরি করা এবং মুছে ফেলা।
অক্টোরি
একটি অক্টরিকে একটি ট্রি ডেটা স্ট্রাকচার হিসাবে সংজ্ঞায়িত করা হয় যেখানে প্রতিটি অভ্যন্তরীণ নোড ঠিক আটটি বাচ্চার সাথে যুক্ত থাকে।
অক্টরিগুলি প্রায়শই একটি 3-মাত্রিক স্থানকে আটটি অক্টেন্টে পুনরাবৃত্তভাবে উপবিভক্ত করার জন্য প্রয়োগ করা হয়।
অক্টরিসকে চতুর্গাছের 3-মাত্রিক অ্যানালগ হিসাবে বিবেচনা করা হয়। নামটি oct + গাছ থেকে তৈরি করা হয়েছে, তবে মনে রাখবেন এটি সাধারণত একটি "t" দিয়ে "octree" লেখা হয়।
Octrees প্রায়ই 3D গ্রাফিক্স এবং 3D গেম ইঞ্জিনে প্রয়োগ করা হয়।
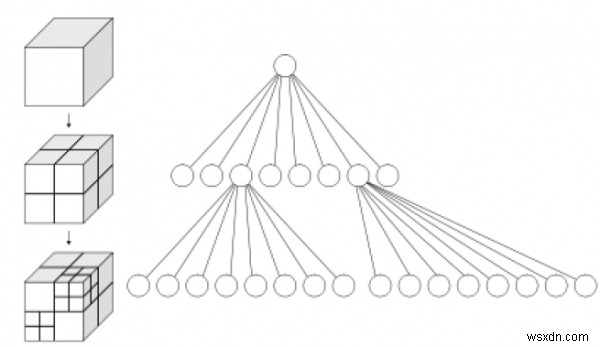
স্থানিক প্রতিনিধিত্বের জন্য
একটি অক্ট্রির প্রতিটি নোড আটটি অক্টেন্টে প্রতিনিধিত্ব করে এমন স্থানকে উপবিভক্ত করার জন্য দায়ী। একটি বিন্দু অঞ্চলে (PR)
octree, নোড একটি সুস্পষ্ট 3-মাত্রিক বিন্দু সঞ্চয় করে, যা সেই নোডের উপবিভাগের "কেন্দ্র"; বিন্দু
আট সন্তানের প্রতিটির জন্য একটি কোণ নির্দিষ্ট করে। একটি ম্যাট্রিক্স ভিত্তিক (MX) অক্টরির ক্ষেত্রে, উপবিভাগ বিন্দুটি নিহিতভাবে নোড দ্বারা উপস্থাপিত স্থানের কেন্দ্র। একটি PR octree এর মূল নোড অসীম স্থান প্রতিনিধিত্ব করতে সক্ষম হতে পারে; একটি MX octree-এর রুট নোড অবশ্যই একটি সীমিত আবদ্ধ স্থান উপস্থাপন করতে সক্ষম হবে যাতে অন্তর্নিহিত কেন্দ্রগুলি ভালভাবে সংজ্ঞায়িত হয়৷
সাধারণ ব্যবহার
- 3D কম্পিউটার গ্রাফিক্সে বিস্তারিত রেন্ডারিংয়ের স্তর
- স্থানিক সূচীকরণ
- নিকটবর্তী প্রতিবেশী খোঁজা হচ্ছে
- তিন মাত্রায় দক্ষ সংঘর্ষ সনাক্তকরণ
- সীমিত উপাদানের বিশ্লেষণ
- স্পার্স ভক্সেল অক্টরি
- রাষ্ট্রের অনুমান
- সেটের অনুমান


