একটি রেঞ্জ ট্রি বিন্দুর একটি তালিকা ধরে রাখার জন্য একটি আদেশকৃত ট্রি ডেটা স্ট্রাকচার হিসাবে সংজ্ঞায়িত করা হয়। এটি একটি প্রদত্ত সীমার মধ্যে সমস্ত পয়েন্টকে দক্ষতার সাথে পুনরুদ্ধার করার অনুমতি দেয় এবং সাধারণত দুই বা উচ্চতর মাত্রায় প্রয়োগ করা হয়। O(log d ) এর দ্রুত ক্যোয়ারী টাইম ছাড়া এটি একটি kd-ট্রির মতই n + k) কিন্তু O(n log d-1 এর আরও খারাপ স্টোরেজ n), d স্থানের মাত্রা নির্দেশ করে, n গাছের বিন্দুর সংখ্যা নির্দেশ করে এবং k একটি প্রদত্ত প্রশ্নের জন্য পুনরুদ্ধার করা পয়েন্টের সংখ্যা নির্দেশ করে। রেঞ্জ ট্রিগুলিকে ব্যবধান গাছের সাথে আলাদা করা যেতে পারে:পয়েন্টগুলি সংরক্ষণ করার পরিবর্তে এবং একটি নির্দিষ্ট পরিসরের পয়েন্টগুলিকে দক্ষতার সাথে পুনরুদ্ধার করার অনুমতি দেওয়ার পরিবর্তে, একটি ব্যবধান গাছ বিরতিগুলি সঞ্চয় করে এবং একটি প্রদত্ত বিন্দু সমন্বিত বিরতিগুলিকে দক্ষতার সাথে পুনরুদ্ধার করার অনুমতি দেয়৷
ডেটা স্ট্রাকচার
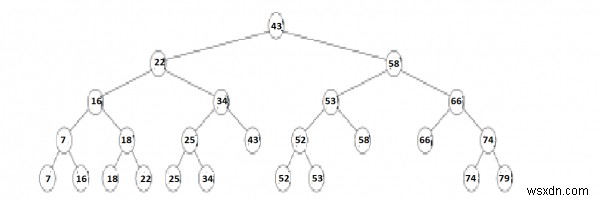
একটি 1-মাত্রিক পরিসরের গাছের উদাহরণ। পাতা ছাড়া অন্য প্রতিটি নোড তার বাম সাবট্রিতে সর্বোচ্চ মান সঞ্চয় করে।
1-মাত্রিক বিন্দুর একটি সেটের একটি রেঞ্জ ট্রি সেই বিন্দুতে একটি সুষম বাইনারি অনুসন্ধান গাছ হিসাবে বিবেচিত হয়। গাছে জমা বিন্দু গাছের পাতায় জমা হয়; প্রতিটি অভ্যন্তরীণ নোড তার বাম সাবট্রিতে থাকা সর্বাধিক মান সংরক্ষণ করে। ডি-ডাইমেনশনে বিন্দুর সেটে একটি রেঞ্জ ট্রি হল একটি পুনরাবৃত্তভাবে সংজ্ঞায়িত মাল্টি-লেভেল বাইনারি সার্চ ট্রি। ডেটা স্ট্রাকচারের প্রতিটি স্তরকে ডি-ডাইমেনশনের একটিতে বাইনারি সার্চ ট্রি হিসাবে বিবেচনা করা হয়। প্রথম স্তরটি ডি-কোঅর্ডিনেটের প্রথমটিতে একটি বাইনারি অনুসন্ধান গাছ। এই গাছের প্রতিটি শীর্ষবিন্দু v একটি যুক্ত কাঠামো নিয়ে গঠিত যা v-এর সাবট্রিতে সঞ্চিত বিন্দুগুলির শেষ (d−1)-অর্ডিনেটের একটি (d−1)-মাত্রিক পরিসরের গাছ।
অপারেশনগুলি
নির্মাণ
n পয়েন্টের একটি সেটে একটি 1-মাত্রিক পরিসরের গাছ হল একটি বাইনারি অনুসন্ধান গাছ, যা O(n log n) সময়ে তৈরি করা যেতে পারে। বিন্দুগুলির প্রথম স্থানাঙ্কে একটি ভারসাম্যপূর্ণ বাইনারি অনুসন্ধান ট্রি তৈরি করে উচ্চ মাত্রার রেঞ্জ ট্রিগুলি পুনরাবৃত্তভাবে তৈরি করা হয় এবং তারপরে, এই গাছের প্রতিটি শীর্ষবিন্দুর জন্য, বিন্দুগুলির উপর একটি (d−1)-মাত্রিক পরিসরের গাছ তৈরি করে। v এর সাবট্রিতে। এইভাবে একটি রেঞ্জ ট্রি তৈরি করতে O(n log d ) প্রয়োজন হবে n) সময়।


