এখানে আমরা দেখব উচ্চতা ব্যালেন্সড লেফটস্ট ট্রিস (HBLT) কী। একটি বাইনারি গাছ বিবেচনা করুন যেখানে একটি বিশেষ নোড, যাকে বহিরাগত নোড বলা হয় প্রতিটি খালি সাবট্রি প্রতিস্থাপন করে। অন্য সব নোডকে বলা হয় অভ্যন্তরীণ নোড . যখন কিছু বাহ্যিক নোড কিছু বাইনারি গাছের সাথে যোগ করা হয়, তখন তাকে বলা হয় বর্ধিত বাইনারি ট্রি .
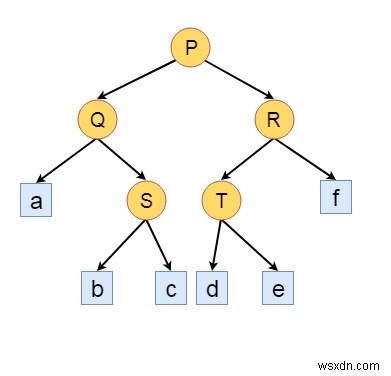
যদি আমরা এই গাছের পাতার প্রান্ত বিবেচনা না করি, তাহলে সেটাই আসল বাইনারি গাছ। এবং এটি বর্ধিত বাইনারি গাছ।
এখন ধরুন s(x) নোড x থেকে এর সাবট্রিতে একটি বহিরাগত নোড পর্যন্ত একটি সংক্ষিপ্ত পথের দৈর্ঘ্য হবে। যদি x একটি বাহ্যিক নোড হয়, তবে এর s(x) মান হল 0৷ যদি x একটি অভ্যন্তরীণ নোড হয়, তাহলে মান হল −
৷ <প্রে>মিন{𝑠(𝐿), 𝑠(𝑅)} + ১এখানে L এবং R হল x এর বাম ও ডান সন্তান। এখন আসুন প্রদত্ত গাছের মান দেখি।
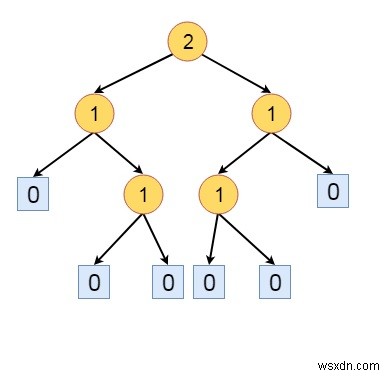
HBLT-এর সংজ্ঞা হল:একটি বাইনারি ট্রি হল একটি উচ্চতা ব্যালেন্সড লেফটিস্ট ট্রি (HBLT), যদি এবং শুধুমাত্র যদি, প্রতিটি অভ্যন্তরীণ নোডে, বাম সন্তানের s মান ডান সন্তানের s মানের থেকে বেশি বা সমান হয়।
উপরের গাছটি HBLT নয়। নোড a, এর প্যারেন্টের s(L) =0 আছে এবং s(R) হল 1, অন্য সব নোডগুলি HBLT-এর নিয়মকে সন্তুষ্ট করছে। তাই যদি আমরা সেই নোডের বাম এবং ডান সাবট্রি, এটিকে HBLT করতে।
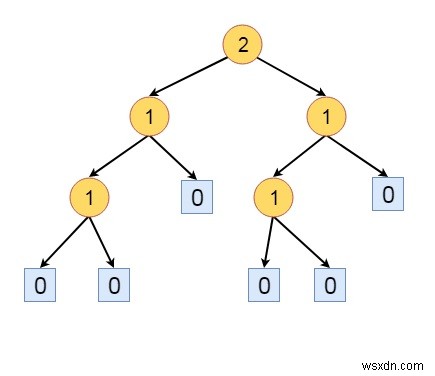
কিছু অন্যান্য সংজ্ঞা হল −
-
সর্বাধিক গাছ (মিনিট ট্রি) হল এমন একটি গাছ, যেখানে প্রতিটি নোডের মান তার বাচ্চাদের তুলনায় বেশি (কম) বা সমান।
-
একটি সর্বাধিক HBLT হল একটি HBLT, এটি একটি সর্বাধিক গাছ, একটি মিনিম HBLT হল একটি HBLT, এটি একটি মিন ট্রিও৷


