একক-উৎস সংক্ষিপ্ততম পথ, নির্বিচারে ওজন

একক উৎস সংক্ষিপ্ত পাথ অ্যালগরিদম (স্বেচ্ছাচারী ওজন ধনাত্মক বা নেতিবাচক জন্য) এছাড়াও পরিচিত বেলম্যান-ফোর্ড অ্যালগরিদম উৎস শীর্ষ থেকে অন্য কোনো শীর্ষে ন্যূনতম দূরত্ব খুঁজে পেতে ব্যবহৃত হয়। ডিজকস্ট্রার অ্যালগরিদমের সাথে এই অ্যালগরিদমের প্রধান পার্থক্য হল, ডিজকস্ট্রার অ্যালগরিদমে আমরা নেতিবাচক ওজন পরিচালনা করতে পারি না, তবে এখানে আমরা সহজেই এটি পরিচালনা করতে পারি।

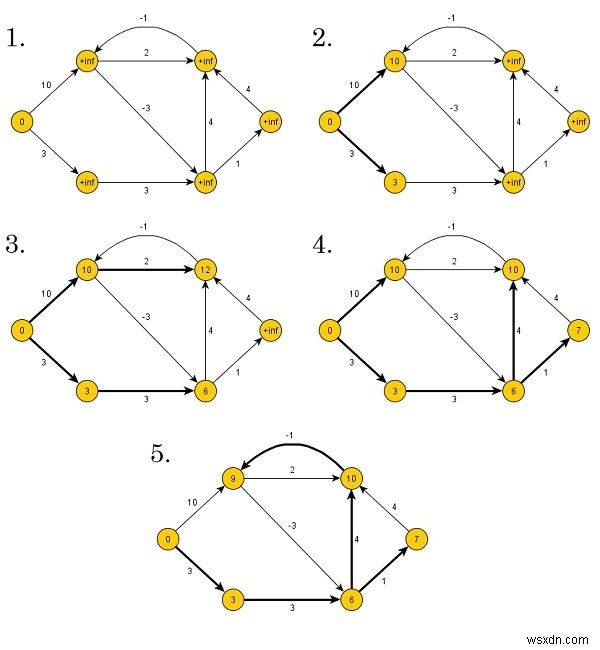
বেলম্যান-ফোর্ড অ্যালগরিদম নীচের উপরে পদ্ধতিতে দূরত্ব খুঁজে পায়। প্রথমে এটি সেই দূরত্বগুলি খুঁজে পায় যেগুলির পথে কেবল একটি প্রান্ত রয়েছে। এর পরে সমস্ত সম্ভাব্য সমাধান খুঁজতে পথের দৈর্ঘ্য বাড়ান।

ইনপুট − গ্রাফের খরচ ম্যাট্রিক্স:

0 6 ∞ 7 ∞
∞ 0 5 8 -4
∞ -2 0 ∞ ∞
∞ ∞ -3 0 9
2 ∞ 7 ∞ 0

আউটপুট − উৎস ভার্টেক্স:2
ভার্ট:0 1 2 3 4
জেলা:-4 -2 0 3 -6
Pred:4 2 -1 0 1
গ্রাফের কোন ঋণাত্মক প্রান্ত চক্র নেই

অ্যালগরিদম

বেলম্যানফোর্ড(dist, pred, উৎস)

ইনপুট − দূরত্ব তালিকা, পূর্বসূরী তালিকা এবং উৎস শীর্ষবিন্দু।

আউটপুট - সত্য, যখন একটি নেতিবাচক চক্র পাওয়া যায়।

Begin
   iCount := 1
   maxEdge := n * (n - 1) / 2 //n is number of vertices
   for all vertices v of the graph, do
      dist[v] := ∞
      pred[v] := ϕ
   done
   dist[source] := 0
   eCount := number of edges present in the graph
   create edge list named edgeList
   while iCount < n, do
   for i := 0 to eCount, do
      if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i)
         dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i)
         pred[edgeList[i].v] := edgeList[i].u
      done
   done
   iCount := iCount + 1
   for all vertices i in the graph, do
      if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i), then
         return true
      done
   return false
End

উদাহরণ(C++)

#include<iostream>
#include<iomanip>
#define V 5
#define INF 999
using namespace std;
//Cost matrix of the graph (directed) vertex 5
int costMat[V][V] = {
   {0, 6, INF, 7, INF},
   {INF, 0, 5, 8, -4},
   {INF, -2, 0, INF, INF},
   {INF, INF, -3, 0, 9},
   {2, INF, 7, INF, 0}
};
typedef struct{
   int u, v, cost;
}edge;
int isDiagraph(){
   //check the graph is directed graph or not
   int i, j;
   for(i = 0; i<V; i++){
      for(j = 0; j<V; j++){
         if(costMat[i][j] != costMat[j][i]){
            return 1;//graph is directed
         }
      }
   }
   return 0;//graph is undirected
}
int makeEdgeList(edge *eList){
   //create edgelist from the edges of graph
   int count = -1;
   if(isDiagraph()){
      for(int i = 0; i<V; i++){
         for(int j = 0; j<V; j++){
            if(costMat[i][j] != 0 && costMat[i][j] != INF){
               count++;//edge find when graph is directed
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }else{
      for(int i = 0; i<V; i++){
         for(int j = 0; j<i; j++){
            if(costMat[i][j] != INF){
               count++;//edge find when graph is undirected
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }
   return count+1;
}
int bellmanFord(int *dist, int *pred,int src){
   int icount = 1, ecount, max = V*(V-1)/2;
   edge edgeList[max];
   for(int i = 0; i<V; i++){
      dist[i] = INF;//initialize with infinity
      pred[i] = -1;//no predecessor found.
   }
   dist[src] = 0;//for starting vertex, distance is 0
   ecount = makeEdgeList(edgeList); //edgeList formation
   while(icount < V){ //number of iteration is (Vertex - 1)
      for(int i = 0; i<ecount; i++){
         if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]){
            //relax edge and set predecessor
            dist[edgeList[i].v] = dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v];
            pred[edgeList[i].v] = edgeList[i].u;
         }
      }
      icount++;
   }
   //test for negative cycle
   for(int i = 0; i<ecount; i++){
      if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]){
         return 1;//indicates the graph has negative cycle
      }
   }
   return 0;//no negative cycle
}
void display(int *dist, int *pred){
   cout << "Vert: ";
   for(int i = 0; i<V; i++)
      cout <<setw(3) << i << " ";
   cout << endl;
   cout << "Dist: ";
   for(int i = 0; i<V; i++)
      cout << setw(3) << dist[i] << " ";
   cout << endl;
   cout << "Pred: ";
   for(int i = 0; i<V; i++)
      cout << setw(3) << pred[i] << " ";
   cout << endl;
}
int main(){
   int dist[V], pred[V], source, report;
   source = 2;
   report = bellmanFord(dist, pred, source);
   cout << "Source Vertex: " << source<<endl;
   display(dist, pred);
   if(report)
      cout << "The graph has a negative edge cycle" << endl;
   else
      cout << "The graph has no negative edge cycle" << endl;
}

আউটপুট

Source Vertex: 2
Vert: 0 1 2 3 4
Dist: -4 -2 0 3 -6
Pred: 4 2 -1 0 1
The graph has no negative edge cycle