এই সমস্যায়, আমাদেরকে n নোডের সাথে একটি অনির্দেশিত সংযুক্ত ট্রি T দেওয়া হয়েছে৷ আমাদের কাজ হল C++-এ একটি গাছে দুটি নন ইন্টারসেক্টিং পাথের সর্বাধিক গুণফল খুঁজে বের করার জন্য একটি প্রোগ্রাম তৈরি করা৷
সমস্যা বর্ণনা − একটি গাছে দুটি ছেদহীন পথের সর্বোচ্চ গুণফল খুঁজে বের করতে। আমরা সমস্ত অ-আকর্ষণীয় পথ খুঁজে বের করব এবং তারপর তাদের দৈর্ঘ্যের গুণফল খুঁজে বের করব।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট
গ্রাফ −
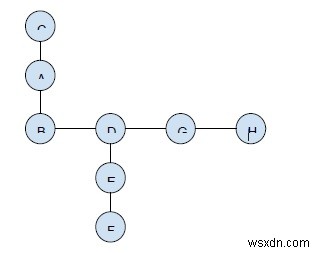
আউটপুট
8
ব্যাখ্যা
ছেদবিহীন পথগুলি যেগুলিকে বিবেচনা করা হয় তা হল C-A-B৷ এবং F-E-D-G-H .
দৈর্ঘ্য 2 এবং 4। পণ্য =8।
সমাধান পদ্ধতি
এই সমস্যার সমাধান হল ডিএফএস ব্যবহার করে গাছটি অতিক্রম করে। এবং আমরা সংযোগ প্রান্ত অপসারণ যদি অনন্য হবে যে পাথ খুঁজুন. এবং তারপরে পথের উপর ঘুরুন এবং এর দৈর্ঘ্য খুঁজে বের করুন। তারপরে আমরা পাথগুলির সাথে জোড়া করব এবং তাদের দৈর্ঘ্যের পণ্যটি খুঁজে বের করব। দুটিকে এমনভাবে বিবেচনা করা হয় যাতে তাদের পণ্য সর্বাধিক হয়।
আমাদের সমাধান বাস্তবায়নের জন্য প্রোগ্রাম,
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
int TreeTraverse(vector<int> graph[], int& currPathMax, int val1, int val2){
int max1 = 0, max2 = 0, maxVal = 0;
for (int i = 0; i < graph[val1].size(); i++) {
if (graph[val1][i] == val2)
continue;
maxVal = max(maxVal, TreeTraverse(graph, currPathMax,
graph[val1][i], val1));
if (currPathMax > max1) {
max2 = max1;
max1 = currPathMax;
}
else
max2 = max(max2, currPathMax);
}
maxVal = max(maxVal, max1 + max2);
currPathMax = max1 + 1;
return maxVal;
}
int FindMaxProductPath(vector<int> graph[], int Size) {
int maxProd = -10;
int pathA, pathB;
int currPathMax, prod;
for (int i = 0; i < Size; i++) {
for (int j = 0; j < graph[i].size(); j++){
currPathMax = 0;
pathA = TreeTraverse(graph, currPathMax, graph[i][j],i);
currPathMax = 0;
pathB = TreeTraverse(graph, currPathMax, i,graph[i][j]);
prod = (pathA * pathB);
maxProd = max(maxProd, prod);
}
}
return maxProd;
}
void insertEdge(vector<int> graph[], int val1, int val2){
graph[val1].push_back(val2);
graph[val2].push_back(val1);
}
int main(){
int Size = 8;
vector<int> graph[Size + 2];
insertEdge(graph, 1, 2);
insertEdge(graph, 2, 4);
insertEdge(graph, 3, 1);
insertEdge(graph, 5, 4);
insertEdge(graph, 7, 8);
insertEdge(graph, 8, 4);
insertEdge(graph, 5, 6);
cout<<"Maximum product of two non-intersecting paths of tree is "<<FindMaxProductPath(graph, Size)<<"\n";
return 0;
} আউটপুট
Maximum product of two non-intersecting paths of tree is 8


