ধরুন আমাদের কিছু নোড এবং সংযুক্ত প্রান্ত সহ একটি গ্রাফ আছে। প্রতিটি প্রান্তের বাইনারি ওজন আছে। সুতরাং ওজন 0 বা 1 হবে। একটি উৎস শীর্ষবিন্দু দেওয়া হয়েছে। আমাদের উৎস থেকে অন্য কোন শীর্ষবিন্দুতে সংক্ষিপ্ততম পথ খুঁজে বের করতে হবে। ধরুন গ্রাফটি নিচের মত -
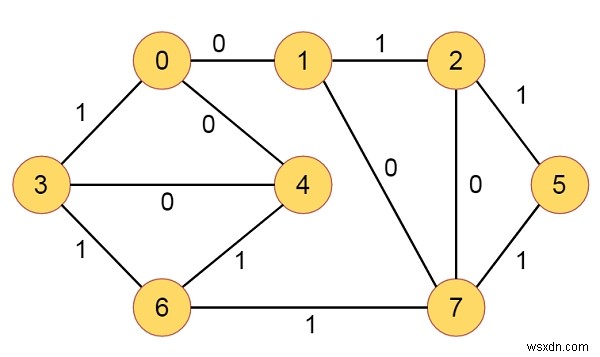
সাধারণ BFS অ্যালগরিদমে সমস্ত প্রান্তের ওজন একই। এখানে কিছু 0 এবং কিছু 1। প্রতিটি ধাপে আমরা সর্বোত্তম দূরত্বের অবস্থা পরীক্ষা করব। এখানে আমরা নোড সংরক্ষণ করতে ডবল শেষ সারি ব্যবহার করব। তাই আমরা প্রান্ত ওজন পরীক্ষা করা হবে. যদি এটি 0 হয়, তবে এটিকে সামনে ধাক্কা দিন, অন্যথায় পিছনে। আরও ভালো ধারণা পেতে আমাদের অ্যালগরিদম পরীক্ষা করা যাক।
অ্যালগরিদম
binaryBFS(src) -
begin define dist array to store source to vertex i into dist[i]. Initially fill with infinity dist[src] := 0 insert src into queue Q. v := first element from Q, and delete it from queue while Q is not empty, do for all connected edge e of v, do if the weight of v to next of i > dist[v] + weight of v to i weight, then update the weight if the weight is 0, then store to front, otherwise back end if done done print all distance from dist array end
উদাহরণ
#include<iostream>
#include<vector>
#include<deque>
#define V 8
using namespace std;
struct node {
int next, weight;
};
vector <node> edges[V];
void binaryBFS(int src) {
int dist[V];
for (int i=0; i<V; i++) //initially set as infinity
dist[i] = INT_MAX;
deque <int> Q;
dist[src] = 0; //distance from source to source is 0
Q.push_back(src);
while (!Q.empty()) {
int v = Q.front(); //delete first vertex, and store to v
Q.pop_front();
for (int i=0; i<edges[v].size(); i++) {
//check optimal distance
if (dist[edges[v][i].next] > dist[v] + edges[v][i].weight) {
dist[edges[v][i].next] = dist[v] + edges[v][i].weight;
if (edges[v][i].weight == 0) //0 weight edge is stored at front, otherwise at back
Q.push_front(edges[v][i].next);
else
Q.push_back(edges[v][i].next);
}
}
}
for (int i=0; i<V; i++)
cout << dist[i] << " ";
}
void addEdge(int u, int v, int wt) {
edges[u].push_back({v, wt});
edges[v].push_back({u, wt});
}
int main() {
addEdge(0, 1, 0);
addEdge(0, 3, 1);
addEdge(0, 4, 0);
addEdge(1, 2, 1);
addEdge(1, 7, 0);
addEdge(2, 5, 1);
addEdge(2, 7, 0);
addEdge(3, 4, 0);
addEdge(3, 6, 1);
addEdge(4, 6, 1);
addEdge(5, 7, 1);
addEdge(6, 7, 1);
int src = 6;
binaryBFS(src);
} আউটপুট
1 1 1 1 1 2 0 1


