একটি নির্দেশিত অ্যাসাইক্লিক গ্রাফে দীর্ঘতম পথ

একটি ওজনযুক্ত নির্দেশিত অ্যাসাইক্লিক গ্রাফ দেওয়া হয়েছে৷ আরেকটি উৎস শীর্ষবিন্দু প্রদান করা হয়. এখন আমাদের গ্রাফে প্রারম্ভিক নোড থেকে অন্য সব শীর্ষবিন্দু পর্যন্ত দীর্ঘতম দূরত্ব খুঁজে বের করতে হবে।

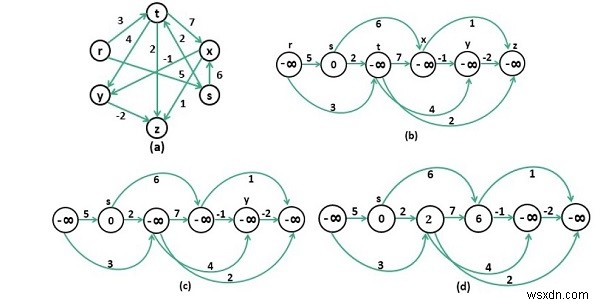
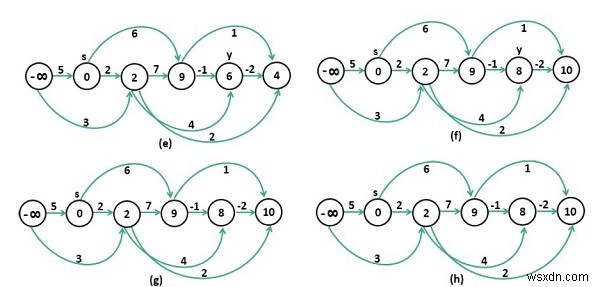
আমাদের টপোলজিকাল সাজানোর কৌশলে নোডগুলিকে সাজাতে হবে এবং টপোলজিকাল সাজানোর পরে ফলাফল একটি স্ট্যাকের মধ্যে সংরক্ষণ করা হয়। তারপরে বারবার স্ট্যাক থেকে পপ করুন এবং প্রতিটি শীর্ষের জন্য দীর্ঘতম দূরত্ব খুঁজে বের করার চেষ্টা করুন৷

ইনপুট এবং আউটপুট

Input:
The cost matrix of the graph.
0  5   3 -∞ -∞ -∞
-∞ 0   2  6 -∞ -∞
-∞ -∞  0  7  4  2
-∞ -∞ -∞  0 -1  1
-∞ -∞ -∞ -∞  0 -2
-∞ -∞ -∞ -∞ -∞  0

Output:
Longest Distance from Source Vertex 1
Infinity 0 2 9 8 10

অ্যালগরিদম

topoSort(u, পরিদর্শন করা, স্ট্যাক)

ইনপুট: প্রারম্ভিক নোড ইউ, ট্র্যাক রাখার জন্য পরিদর্শন তালিকা, স্ট্যাক।

আউটপুট - টপোলজিক্যাল উপায়ে নোডগুলি সাজান৷

Begin
   mark u as visited
   for all vertex v, which is connected with u, do
      if v is not visited, then
         topoSort(v, visited, stack)
   done
   push u into the stack
End

দীর্ঘতম পথ(শুরু)

ইনপুট - প্রারম্ভিক নোড।

আউটপুট - প্রারম্ভিক নোড থেকে সমস্ত শীর্ষবিন্দুর দীর্ঘতম দূরত্বের তালিকা৷

Begin
   initially make all nodes as unvisited
   for each node i, in the graph, do
      if i is not visited, then
         topoSort(i, visited, stack)
   done

   make distance of all vertices as - ∞
   dist[start] := 0
   while stack is not empty, do
      pop stack item and take into nextVert
      if dist[nextVert] ≠ - ∞, then
         for each vertices v, which is adjacent with nextVert, do
            if cost[nextVert, v] ≠ - ∞, then
               if dist[v] < dist[nectVert] + cost[nextVert, v], then
                  dist[v] := dist[nectVert] + cost[nextVert, v]
         done
   done

   for all vertices i in the graph, do
      if dist[i] = - ∞, then
         display Infinity
      else
         display dist[i]
   done
End

উদাহরণ

#include<iostream>
#include<stack>
#define NODE 6
#define INF -9999
using namespace std;

int cost[NODE][NODE] = {
   {0, 5, 3, INF, INF, INF},
   {INF, 0, 2, 6, INF, INF},
   {INF, INF, 0, 7, 4, 2},
   {INF, INF, INF, 0, -1, 1},
   {INF, INF, INF, INF, 0, -2},
   {INF, INF, INF, INF, INF, 0}
};

void topoSort(int u, bool visited[], stack<int>&stk) {
   visited[u] = true;    //set as the node v is visited

   for(int v = 0; v<NODE; v++) {
      if(cost[u][v]) {    //for allvertices v adjacent to u
         if(!visited[v])
            topoSort(v, visited, stk);
      }
   }

   stk.push(u);    //push starting vertex into the stack
}

void longestPath(int start) {
   stack<int> stk;
   int dist[NODE];
   bool vis[NODE];

   for(int i = 0; i<NODE;i++)
      vis[i] = false;    // make all nodes as unvisited at first
         
   for(int i = 0; i<NODE; i++)    //perform topological sort for vertices
      if(!vis[i])
         topoSort(i, vis, stk);
               
   for(int i = 0; i<NODE; i++)
      dist[i] = INF;    //initially all distances are infinity
   dist[start] = 0;    //distance for start vertex is 0
   
   while(!stk.empty()) {    //when stack contains element, process in topological order
      int nextVert = stk.top(); stk.pop();

      if(dist[nextVert] != INF) {
         for(int v = 0; v<NODE; v++) {
            if(cost[nextVert][v] && cost[nextVert][v] != INF) {
               if(dist[v] < dist[nextVert] + cost[nextVert][v])
                  dist[v] = dist[nextVert] + cost[nextVert][v];
            }
         }
      }
   }
     
   for(int i = 0; i<NODE; i++)
      (dist[i] == INF)?cout << "Infinity ":cout << dist[i]<<" ";
}

main() {
   int start = 1;
   cout << "Longest Distance From Source Vertex "<<start<<endl;
   longestPath(start);
}

আউটপুট

Longest Distance From Source Vertex 1
Infinity 0 2 9 8 10