পাইথন ব্যবহার করে লিনিয়ার রিগ্রেশন?

যা আমরা একটি ব্যাখ্যামূলক পরিবর্তনশীল হিসাবে আউটডোর এয়ার টেম্পারেচার (OAT) ব্যবহার করে একটি বিল্ডিংয়ের শক্তি মডেল করতে ব্যবহার করতে যাচ্ছি৷

যে ফোল্ডারে আমাদের জুপিটার বা IDE ইনস্টল করা আছে সেখানে csv ফাইলটি সংরক্ষণ করুন।

প্রয়োজনীয় লাইব্রেরি এবং ডেটাসেট আমদানি করুন

প্রথমে আমরা প্রয়োজনীয় লাইব্রেরি আমদানি করতে যাচ্ছি এবং তারপর পান্ডাস পাইথন লাইব্রেরি ব্যবহার করে ডেটাসেট পড়তে যাচ্ছি।

# Importing Necessary Libraries

import pandas as pd
#Required for numerical functions
import numpy as np
from scipy import stats
from datetime import datetime
from sklearn import preprocessing
from sklearn.model_selection import KFold
from sklearn.linear_model import LinearRegression
#For plotting the graph
import matplotlib.pyplot as plt
%matplotlib inline

# Reading Data
df = pd.read_csv('building1retail.csv', index_col=[0],
date_parser=lambda x: datetime.strptime(x, "%m/%d/%Y %H:%M"))
df.head()

আউটপুট

ডেটাসেট অন্বেষণ

তাই আসুন প্রথমে আমাদের ডেটাসেটকে পান্ডাদের সাথে প্লট করে কল্পনা করি।

df.plot(figsize=(22,6))

আউটপুট

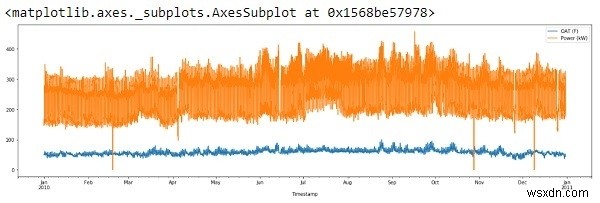
সুতরাং, x-অক্ষ Jan2010 – Jan2011 এর ডেটা দেখাচ্ছে।

যদি আমরা উপরের আউটপুটটি দেখি, আমরা লক্ষ্য করতে পারি যে প্লট সম্পর্কে দুটি অদ্ভুত জিনিস রয়েছে:

• কোনো অনুপস্থিত ডেটা নেই বলে মনে হচ্ছে, এটি পরীক্ষা করতে, শুধু চালান:

df.isnull().values.any()

আউটপুট

False

মিথ্যা ফলাফল আমাদের বলছে ডেটাফ্রেমে কোন শূন্য মান নেই।

• মনে হচ্ছে, ডেটাতে কিছু অসঙ্গতি আছে (দীর্ঘ নিম্নগামী স্পাইক)

অসামঞ্জস্য বা 'আউটলিয়ার' সাধারণত একটি পরীক্ষামূলক ত্রুটির ফলাফল বা সত্যিকারের মান হতে পারে। উভয় ক্ষেত্রেই, আমরা এটি বাতিল করতে যাচ্ছি কারণ তারা রিগ্রেশন লাইনের ঢালকে মারাত্মকভাবে প্রভাবিত করে৷

আমরা 'আউটলায়ার্স' বাতিল করার আগে, প্রথমে আমাদের ডেটা কী ধরনের বিতরণ প্রতিনিধিত্ব করছে তা পরীক্ষা করা যাক:

df.hist()

আউটপুট

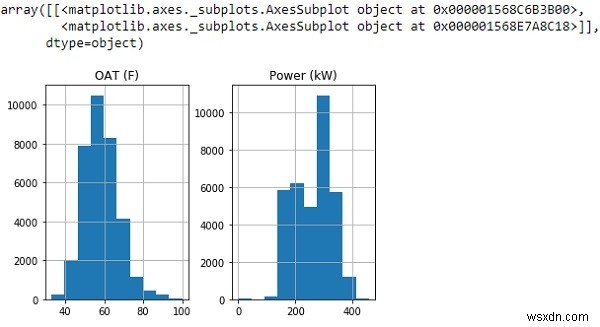
উপরের হিস্টোগ্রাম থেকে, আমরা দেখতে পাচ্ছি যে আমাদের গ্রাফটি এমন ডেটা দেখাচ্ছে যা মোটামুটি একটি স্বাভাবিক বিতরণকে অনুসরণ করে।

তাই আসুন গড় থেকে 3টি স্ট্যান্ডার্ড বিচ্যুতির বেশি সমস্ত মান বাদ দেই এবং নতুন ডেটাফ্রেম প্লট করি৷

std_dev = 3
df = df[(np.abs(stats.zscore(df)) < float(std_dev)).all(axis=1)]
df.plot(figsize=(22, 6))

আউটপুট

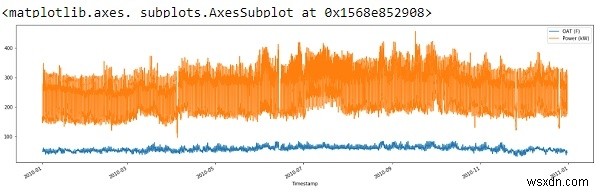
সুতরাং উপরের আউটপুট থেকে আমরা দেখতে পাচ্ছি, আমরা কিছু পরিমাণে স্পাইকগুলি সরিয়ে দিয়েছি এবং আমাদের ডেটা পরিষ্কার করেছি৷

রৈখিক সম্পর্ক যাচাই করুন

OAT এবং পাওয়ারের মধ্যে কোন রৈখিক সম্পর্ক আছে কিনা তা খুঁজে বের করতে, আসুন একটি সাধারণ স্ক্যাটার প্লট প্লট করি:

plt.scatter(df['OAT (F)'], df['Power (kW)'])

আউটপুট

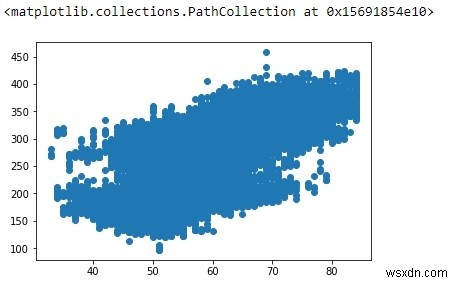
লিনিয়ার রিগ্রেশন

মডেল চালানোর জন্য এবং এর কার্যক্ষমতা মূল্যায়ন করতে আমরা Scikit-learn মডিউল ব্যবহার করতে যাচ্ছি, আমরা k-folds ক্রস ভ্যালিডেশন (k=3) ব্যবহার করতে যাচ্ছি আমাদের মডেলের কর্মক্ষমতা মূল্যায়ন করতে।

X = pd.DataFrame(df['OAT (F)'])
y = pd.DataFrame(df['Power (kW)'])
model = LinearRegression()
scores = []
kfold = KFold(n_splits=3, shuffle=True, random_state=42)
for i, (train, test) in enumerate(kfold.split(X, y)):
model.fit(X.iloc[train,:], y.iloc[train,:])
score = model.score(X.iloc[test,:], y.iloc[test,:])
scores.append(score)
print(scores)

আউটপুট

[0.38768927735902703, 0.3852220878090444, 0.38451654781487116]

উপরের প্রোগ্রামে, মডেল =LinearRegression() একটি লিনিয়ার রিগ্রেশন মডেল তৈরি করে এবং for loop ডেটাসেটটিকে তিনটি ভাঁজে ভাগ করে। তারপর লুপের ভিতরে, আমরা ডেটা ফিট করি এবং তারপর একটি তালিকায় এর স্কোর যুক্ত করে এর কার্যকারিতা মূল্যায়ন করি।

যাইহোক, ফলাফলগুলি ভাল দেখাচ্ছে না এবং আমরা এটির কার্যকারিতা উন্নত করতে পারি।

দিনের সময়

শক্তি (পরিবর্তনশীল) দিনের সময়ের উপর অত্যন্ত নির্ভরশীল। আসুন এক-হট এনকোডিং ব্যবহার করে আমাদের রিগ্রেশন মডেলে এটিকে অন্তর্ভুক্ত করতে এই তথ্যটি ব্যবহার করি৷

model = LinearRegression()
scores = []
kfold = KFold(n_splits=3, shuffle=True, random_state=42)
for i, (train, test) in enumerate(kfold.split(X, y)):
   model.fit(X.iloc[train,:], y.iloc[train,:])
   scores.append(model.score(X.iloc[test,:], y.iloc[test,:]))
print(scores)

আউটপুট

[0.8074246958895391, 0.8139449185141592, 0.8111379602960773]

আমাদের মডেলে এটি একটি বড় পার্থক্য।

সারাংশ

এই বিভাগে, আমরা একটি ডেটাসেট অন্বেষণ এবং এটিকে একটি রিগ্রেশন মডেলের সাথে মানানসই করার জন্য প্রস্তুত করার প্রাথমিক বিষয়গুলি শিখেছি৷ আমরা এর কার্যকারিতা মূল্যায়ন করেছি, এর ত্রুটিগুলি সনাক্ত করেছি এবং এটি ঠিক করেছি৷