পাইথন প্রোগ্রাম কত কিউব কাটা হয় তা খুঁজে বের করতে

ধরুন, a, b, এবং c এর কয়েকটি কিউব রয়েছে এবং সেগুলো ব্যবহার করে axbxc মাত্রার একটি নতুন বক্স তৈরি করা হয়েছে। a, b, এবং c হল যুগলভিত্তিক সহ-প্রধান; gcd(a, b) =gcd(b,c) =gcd(c, d) =1. ছবিতে দেখানো হিসাবে আমাদের একটি একক স্লাইস দিয়ে বক্সটিকে দুটি টুকরো করতে হবে। আমাদের খুঁজে বের করতে হবে বক্সটি এভাবে কাটলে কত কিউব করে দুই টুকরো করা হয়। আমাদের একটি অ্যারে দেওয়া হয়েছে যাতে সম্ভাব্য তিনটি মাত্রা রয়েছে এবং আমাদের সেই থেকে আমাদের উত্তর খুঁজে বের করতে হবে৷

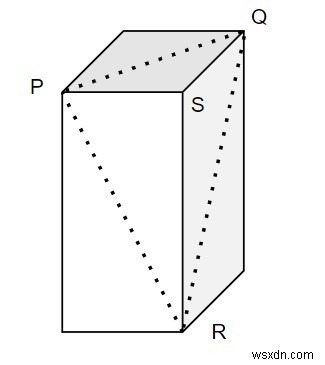
কাটাটি এভাবে করা হয় যে এটি প্লেনটি পি, কিউ এবং আর শীর্ষবিন্দু দিয়ে যাচ্ছে।

সুতরাং, যদি ইনপুটটি n =3, input_array =[[1, 2, 3], [4, 2, 5], [6, 8, 2]] হয়, তাহলে আউটপুট হবে [5, 18, 37] ]

এখানে 3টি ভিন্ন দৃষ্টান্ত দেওয়া হয়েছে এবং আমাদের কাটা সংখ্যা বের করতে হবে। যদি ছবিতে দেখানো উপায়ে কিউব কাটা হয়; 5, 16, এবং 37 কিউব যথাক্রমে কাটা হয়।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব &miuns;

• আউটপুট :=একটি নতুন তালিকা
• আমি 0 থেকে n রেঞ্জের জন্য, কর
  • a :=input_array[i, 0]
  • b :=input_array[i, 1]
  • c :=input_array[i, 2]
  • val :=ফ্লোর মান (a * b + a * c + b * c - 1) / 2 মোড 1000000007
  • আউটপুটের শেষে val সন্নিবেশ করান
• রিটার্ন আউটপুট

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

from math import ceil
def solve(n, input_array):
   output = []
   for i in range(n):
      a, b, c = input_array[i][0], input_array[i][1], input_array[i][2]
      val = ((a * b + a * c + b * c - 1) // 2 % 1000000007)
      output.append(val)
   return output
print(solve(3, [[1, 2, 3], [4, 2, 5], [6, 8, 2]]))

ইনপুট

3, [[1, 2, 3], [4, 2, 5], [6, 8, 2]]

আউটপুট

[5, 18, 37]