পাইথনের গোডাউনে কতগুলি বাক্স রাখা যায় তা খুঁজে বের করার প্রোগ্রাম

ধরুন, আমাদের পূর্ণসংখ্যা সম্বলিত দুটি অ্যারে আছে। একটি তালিকায় কিছু ইউনিট প্রস্থ বাক্সের উচ্চতা রয়েছে এবং অন্য অ্যারেতে গোডাউনের কক্ষের উচ্চতা রয়েছে। কক্ষগুলি 0...n নম্বরযুক্ত, এবং কক্ষগুলির উচ্চতা অ্যারের গোডাউনে তাদের নিজ নিজ সূচীতে দেওয়া আছে। গুদামে ঠেলে দেওয়া যাবে এমন বাক্সের সংখ্যা বের করতে হবে। কিছু জিনিস মাথায় রাখতে হবে,

বাক্সগুলি একটির উপর আরেকটি রাখা যাবে না।
বাক্সের ক্রম পরিবর্তন করা যেতে পারে।

বাক্সগুলি যে কোনও দিক থেকে গোডাউনে রাখা হয়, এটি বাম বা ডান দিক হতে পারে। যদি একটি বাক্স ঘরের উচ্চতার চেয়ে লম্বা হয়, তবে বাক্সটি তার ডানদিকের সমস্ত বাক্স সহ গোডাউনে ঠেলে দেওয়া যাবে না।

সুতরাং, যদি ইনপুটটি বক্সের মতো হয় =[4, 5, 6], গোডাউন =[4, 5, 6, 7], তাহলে আউটপুট হবে 3 ইনপুট হিসাবে দেওয়া তিনটি বাক্সই গোডাউনে রাখা যেতে পারে।

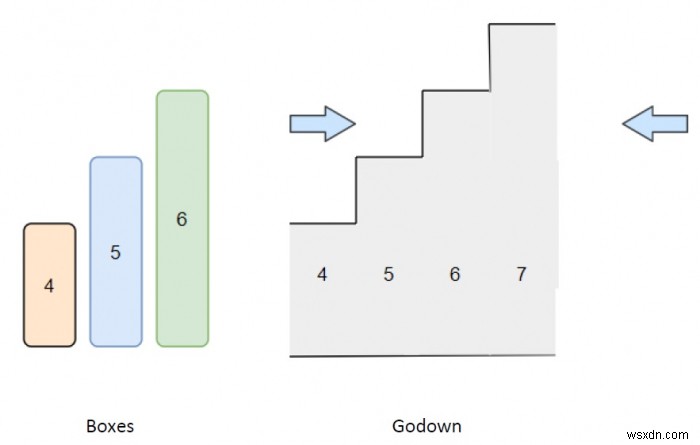
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

তালিকা বাক্সগুলিকে একটি অবতরণ ক্রমে সাজান
l :=0
r :=গোডাউনের আকার - 1
bi :=0
ret :=0
যখন bi <বাক্সের আকার এবং l <=r, do
- যদি গোডাউন[l]> গোডাউন[r], তাহলে
  - যদি বাক্সগুলি [bi] <=গোডাউন[l], তাহলে
    - ret :=ret + 1
    - l :=l + 1
  - অন্যথায়,
    - যদি বাক্সগুলি [bi] <=গোডাউন[r], তাহলে
      - ret :=ret + 1
      - r :=r - 1
  - bi :=bi + 1
রিটার্ন রিটার্ন

উদাহরণ (পাইথন)

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def solve(boxes, godown):
   boxes.sort(reverse = True)

   l, r = 0, len(godown) - 1
   bi, ret = 0, 0
   while bi < len(boxes) and l <= r:
      if godown[l] > godown[r]:
         if boxes[bi] <= godown[l]:
            ret += 1
            l += 1
      else:
         if boxes[bi] <= godown[r]:
            ret += 1
            r -= 1
      bi += 1

   return ret

print(solve([4, 5, 6], [4, 5, 6, 7]))

ইনপুট

[4, 5, 6], [4, 5, 6, 7]