পাইথনে একটি এন-আরি গাছের ব্যাস খুঁজে বের করার প্রোগ্রাম

ধরুন, আমাদের একটি n-ary গাছ দেওয়া হল এবং গাছের ব্যাস নির্ধারণ করতে বলা হল। গাছের ব্যাস হল দীর্ঘতম পথ যা গাছের যেকোনো দুটি পাতার নোডের মধ্যে বিদ্যমান। আমাদের খুঁজে বের করতে হবে এবং পূর্ণসংখ্যার মানটি ফেরত দিতে হবে যা গাছের ব্যাসকে প্রতিনিধিত্ব করে।

সুতরাং, যদি ইনপুট মত হয়

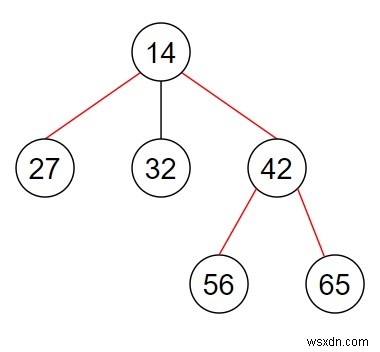
তাহলে আউটপুট হবে 3.

এই n-ary গাছের ব্যাস 27->14, 14->42, এবং 42->56 বা 42->65 (লাল রেখা দ্বারা চিত্রে চিহ্নিত) প্রান্তগুলি নিয়ে গঠিত। পথের দৈর্ঘ্য 3.

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• উত্তর :=1

• একটি ফাংশন depth() সংজ্ঞায়িত করুন। এটি রুট নেবে

  • যদি রুট খালি না হয়, তাহলে

    • রিটার্ন 0

  • শিশু :=0, 0

    মান ধারণকারী একটি নতুন তালিকা

  • temp_children :=একটি নতুন তালিকা

  • মূলের শিশুদের মধ্যে প্রতিটি শিশুর জন্য, করুন

    • temp_children

      এর শেষে গভীরতা(শিশু) সন্নিবেশ করান

  • যদি (temp_children)> 0 এর আকার, তাহলে

    • শিশু :=temp_children

  • উত্তর :=সর্বাধিক উত্তর, যোগফল (তালিকা বাছাই করা শিশুদের [(শিশুদের সূচকের দৈর্ঘ্য থেকে)- 2 শেষ পর্যন্ত]) + 1

  • সর্বাধিক বাচ্চাদের ফেরত + 1

• গভীরতা(মূল)

• ফেরত (উত্তর -1)

উদাহরণ (পাইথন)

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

ক্লাস নোড:def __init__(self, value, child =None) -> None:self.val =value self.children =[] if child !=None:for value in child:self.children.append(value) )ans =1def solve(root):def depth(root):global ans যদি রুট না হয়:রিটার্ন 0 Children =[0, 0] temp_children =[depth(child) in child in root.children] if len(temp_children)> 0:Children =temp_children ans =max(ans, sum(sorted(children)[-2:]) + 1) রিটার্ন max(children) + 1 depth(root) রিটার্ন উত্তর -1node6 =Node(65)node5 =Node( 56)node4 =Node(42, [node5, node6])node3 =Node(32)node2 =Node(27)node1 =Node(14, [node2, node3, node4])root =node1print(solve(root)) 
ইনপুট
 
node6 =Node(65)node5 =Node(56)node4 =Node(42, [node5, node6])node3 =Node(32)node2 =Node(27)node1 =Node(14, [node2, node3, node4])root =node1
 
আউটপুট
 
3