পাইথনে একটি এন-আরি গাছের দীর্ঘতম পথের দৈর্ঘ্য খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের একটি প্রান্ত তালিকা আছে যেখানে প্রতিটি আইটেম ধরে আছে (u, v) প্রতিনিধিত্ব করে u হল v এর মূল। আমাদের গাছের দীর্ঘতম পথের দৈর্ঘ্য খুঁজে বের করতে হবে। পথের দৈর্ঘ্য হল 1 + সেই পথে নোডের সংখ্যা।

সুতরাং, যদি ইনপুট মত হয়

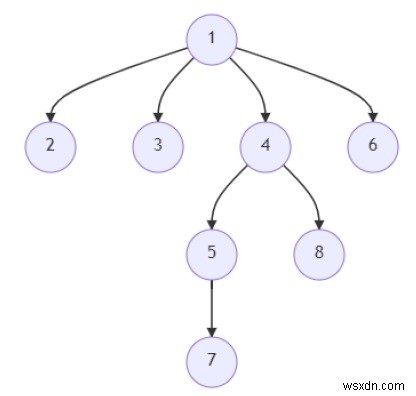
তাহলে আউটপুট হবে 5, কারণ পাথ হল [1, 4, 5, 7], মোট 4টি নোড আছে, তাই পাথের দৈর্ঘ্য হল 1 + 4 =5৷

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

g :=প্রদত্ত প্রান্ত তালিকা থেকে গ্রাফের সংলগ্ন তালিকা
d :=একটি নতুন মানচিত্র
একটি ফাংশন bfs() সংজ্ঞায়িত করুন। এটি o
d[o] :=1
f :=o
q :=[o]
q এর প্রতিটি x এর জন্য, করুন
- g[x] এ প্রতিটি y এর জন্য, করুন
  - যদি y d-এ না থাকে, তাহলে
    - d[y] :=d[x] + 1
    - যদি d[y]> d[f] হয়, তাহলে
      - f :=y
    - q তে y ঢোকান
রিটার্ন f
প্রধান পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন -
g এর প্রতিটি o এর জন্য, করুন
- f :=bfs(o)
- d :=একটি নতুন মানচিত্র
- রিটার্ন d[bfs(f)]
রিটার্ন 0

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def solve(edges):
   g = {}
   for u, v in edges:
      if u not in g:
         g[u] = []
      g[u] += (v,)
      if v not in g:
         g[v] = []
      g[v] += (u,)
   d = {}

   def bfs(o):
      d[o] = 1
      f = o
      q = [o]
      for x in q:
         for y in g[x]:
            if y not in d:
               d[y] = d[x] + 1
               if d[y] > d[f]:
                  f = y
               q += (y,)
      return f

   for o in g:
      f = bfs(o)
      d = {}
      return d[bfs(f)]
   return 0

edges = [(1, 2),(1, 3),(1, 4),(4, 5),(5,7),(1,6),(4,8)]
print(solve(edges))

ইনপুট

[(1, 2),(1, 3),(1, 4),(4, 5),(5,7),(1,6),(4,8)]