পাইথনে সমস্ত পয়েন্ট সংযোগ করার জন্য সর্বনিম্ন খরচ খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের কাছে পয়েন্ট নামক একটি অ্যারে আছে যার ফর্মে কিছু বিন্দু রয়েছে (x, y)। এখন দুটি বিন্দু (xi, yi) এবং (xj, yj) সংযোগ করার খরচ তাদের মধ্যে ম্যানহাটান দূরত্ব, সূত্রটি হল |xi - xj| + |yi - yj|। সমস্ত পয়েন্ট সংযুক্ত করার জন্য আমাদের সর্বনিম্ন খরচ খুঁজে বের করতে হবে।

সুতরাং, ইনপুট যদি পয়েন্টের মত হয় =[(0,0),(3,3),(2,10),(6,3),(8,0)], তাহলে আউটপুট হবে 22 কারণ

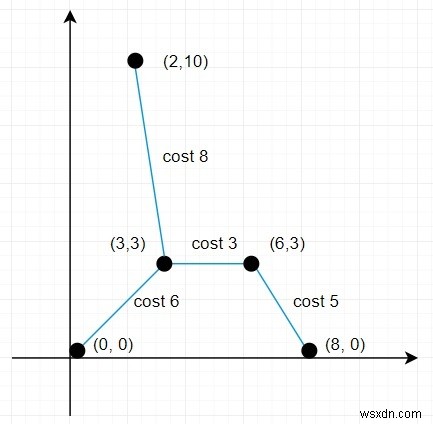
সুতরাং এখানে মোট দূরত্ব হল (6+5+3+8) =22।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

পয়েন্ট_সেট :=একটি নতুন সেট ধারণ করে সংখ্যা 0 থেকে পয়েন্টের আকার পর্যন্ত - 1
স্তূপ :=জোড়া দিয়ে একটি গাদা তৈরি করুন (0, 0)
visited_node :=একটি নতুন সেট
মোট_দূরত্ব :=0
যদিও হিপ খালি না থাকে এবং পরিদর্শন_নোডের আকার <পয়েন্টের আকার, কর
- (দূরত্ব, বর্তমান_সূচক) :=গাদা থেকে উপাদান মুছুন
- যদি visited_node-এ current_index না থাকে, তাহলে
  - ভিজিটেড_নোডে কারেন্ট_ইনডেক্স ঢোকান
  - পয়েন্ট_সেট থেকে বর্তমান_সূচক মুছুন
  - মোট_দূরত্ব :=মোট_দূরত্ব + দূরত্ব
  - (x0, y0) :=পয়েন্ট[কারেন্ট_ইনডেক্স]
  - পয়েন্ট_সেটে প্রতিটি পরবর্তী_সূচকের জন্য, করুন
    - (x1, y1) :=পয়েন্ট[পরবর্তী_সূচক]
    - ঢোকান (|x0 - x1| + |y0 - y1| , next_index) স্তূপে
মোট_দূরত্ব ফেরত দিন

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

import heapq
def solve(points):
   points_set = set(range(len(points)))
   heap = [(0, 0)]
   visited_node = set()
   total_distance = 0
   while heap and len(visited_node) < len(points):
      distance, current_index = heapq.heappop(heap)
      if current_index not in visited_node:
         visited_node.add(current_index)
         points_set.discard(current_index)
         total_distance += distance
         x0, y0 = points[current_index]
         for next_index in points_set:
            x1, y1 = points[next_index]
            heapq.heappush(heap, (abs(x0 - x1) + abs(y0 - y1), next_index))
   return total_distance
points = [(0,0),(3,3),(2,10),(6,3),(8,0)]
print(solve(points))

ইনপুট

[(0,0),(3,3),(2,10),(6,3),(8,0)]