পাইথন ব্যবহার করে সমস্ত নোডে পৌঁছানোর জন্য ন্যূনতম সংখ্যক শীর্ষবিন্দু খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের একটি নির্দেশিত অ্যাসাইক্লিক গ্রাফ রয়েছে, যেখানে n শীর্ষবিন্দু এবং নোডগুলি 0 থেকে n-1 পর্যন্ত সংখ্যাযুক্ত, গ্রাফটি একটি প্রান্ত তালিকা দ্বারা প্রতিনিধিত্ব করা হয়, যেখানে প্রান্তগুলি [i] =(u, v) নোড থেকে u থেকে একটি নির্দেশিত প্রান্তকে প্রতিনিধিত্ব করে নোড v. আমাদের শীর্ষবিন্দুর ক্ষুদ্রতম সেট খুঁজে বের করতে হবে যেখান থেকে গ্রাফের সমস্ত নোড পৌঁছানো যায়। (আমরা যে কোন ক্রমে শীর্ষবিন্দু ফেরত দিতে পারি)।

সুতরাং, যদি ইনপুট মত হয়

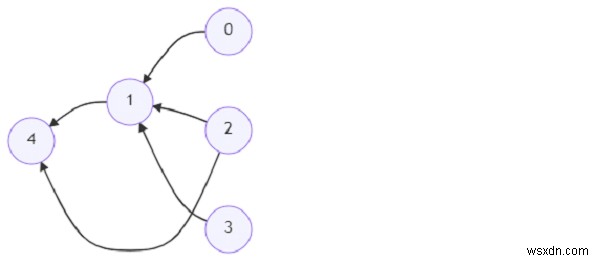
তাহলে আউটপুট হবে [0,2,3] কারণ এই দুটি শীর্ষবিন্দু অন্য কোনো শীর্ষবিন্দু থেকে পৌঁছানো সম্ভব নয়, তাই যদি আমরা এগুলি থেকে শুরু করি তাহলে আমরা সব কভার করতে পারব।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• n :=প্রান্তের আকার

• all_nodes :=রেঞ্জ 0 থেকে n

  একটি নতুন সেট

• v :=একটি নতুন সেট

• প্রতিটি প্রান্তের জন্য (i, j) প্রান্তে, করুন

  • v

    -এ j যোগ করুন

• উত্তর :=all_nodes থেকে সমস্ত সাধারণ প্রান্ত এবং v all_nodes থেকে সরিয়ে দিন

• উত্তর ফেরত দিন

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

def solve(edges):
   n = len(edges)
   all_nodes = set(range(n))
   v = set()
   for edge in edges:
      v.add(edge[1])
   ans = all_nodes - v
   return ans
edges = [(0,1),(2,1),(3,1),(1,4),(2,4)]
print(solve(edges))

ইনপুট

[(0,1),(2,1),(3,1),(1,4),(2,4)]

আউটপুট

{0, 2, 3}