এই সমস্যায়, আমাদের একটি বাইনারি ট্রি দেওয়া হয় এবং আমাদের Q প্রশ্ন দেওয়া হয়। আমাদের কাজ হল C++-এ বাইনারি ট্রি- O(logn) পদ্ধতির দুই নোডের মধ্যে দূরত্ব খুঁজে বের করার জন্য প্রশ্নের সমাধান করার জন্য একটি প্রোগ্রাম তৈরি করা।
সমস্যা বর্ণনা
প্রতিটি ক্যোয়ারীতে, আমাদেরকে বাইনারি ট্রির দুটি নোড দেওয়া হয় এবং আমাদের দুটি নোডের মধ্যে সংখ্যার দূরত্ব খুঁজে বের করতে হবে অর্থাৎ একটি নোড থেকে অন্য নোডে পৌঁছানোর জন্য প্রান্তের সংখ্যা কত হবে৷
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট :বাইনারি ট্রি
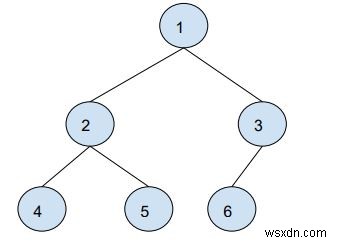
প্রশ্ন =3
প্রশ্ন 1 -> [2, 6]
Q2 -> [4, 1]
Q3 -> [5, 3]
আউটপুট: 3, 2, 3
সমাধান পদ্ধতি
সমস্যা সমাধানের জন্য, আমরা দূরত্ব সূত্র ব্যবহার করব যা সর্বনিম্ন সাধারণ পূর্বপুরুষ (LCA) এবং তাদের দূরত্ব ব্যবহার করে।
দূরত্ব(n1, n2) =দূরত্ব(root,n1) + দূরত্ব(root,n1) - 2 * দূরত্ব(root,LCA)
সমস্যা সমাধানের জন্য এই ধাপগুলি অনুসরণ করতে হবে,
-
প্রতিটি নোডের স্তর খুঁজুন যেমন N1, N2, LCA।
-
তারপর আমরা অয়লারের ট্যুরফ ট্রির উপর ভিত্তি করে বাইনারি গাছের অ্যারে খুঁজে পাব।
-
তারপর আমরা LCA-এর জন্য একটি সেগমেন্ট ট্রি তৈরি করব।
উদাহরণ
#include <bits/stdc++.h>
#define MAX 1000
using namespace std;
int eulerArray[MAX];
int eIndex = 0;
int vis[MAX];
int L[MAX];
int H[MAX];
int level[MAX];
struct Node {
int data;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int data) {
struct Node* temp = new struct Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void FindNodeLevels(struct Node* root) {
if (!root)
return;
queue<pair<struct Node*, int> > q;
q.push({ root, 0 });
pair<struct Node*, int> p;
while (!q.empty()) {
p = q.front();
q.pop();
level[p.first->data] = p.second;
if (p.first->left)
q.push({ p.first->left, p.second + 1 });
if (p.first->right)
q.push({ p.first->right, p.second + 1 });
}
}
void createEulerTree(struct Node* root) {
eulerArray[++eIndex] = root->data;
if (root->left) {
createEulerTree(root->left);
eulerArray[++eIndex] = root->data;
}
if (root->right) {
createEulerTree(root->right);
eulerArray[++eIndex] = root->data;
}
}
void creareEulerArray(int size) {
for (int i = 1; i <= size; i++) {
L[i] = level[eulerArray[i]];
if (vis[eulerArray[i]] == 0) {
H[eulerArray[i]] = i;
vis[eulerArray[i]] = 1;
}
}
}
pair<int, int> seg[4 * MAX];
pair<int, int> min(pair<int, int> a, pair<int, int> b) {
if (a.first <= b.first)
return a;
else
return b;
}
pair<int, int> buildSegTree(int low, int high, int pos) {
if (low == high) {
seg[pos].first = L[low];
seg[pos].second = low;
return seg[pos];
}
int mid = low + (high - low) / 2;
buildSegTree(low, mid, 2 * pos);
buildSegTree(mid + 1, high, 2 * pos + 1);
seg[pos] = min(seg[2 * pos], seg[2 * pos + 1]);
}
pair<int, int> LCA(int qlow, int qhigh, int low, int high, int pos) {
if (qlow <= low && qhigh >= high)
return seg[pos];
if (qlow > high || qhigh < low)
return { INT_MAX, 0 };
int mid = low + (high - low) / 2;
return min(LCA(qlow, qhigh, low, mid, 2 * pos), LCA(qlow, qhigh,mid + 1, high, 2 * pos +1));
}
int CalcNodeDistance(int node1, int node2, int size) {
int prevn1 = node1, prevn2 = node2;
node1 = H[node1];
node2 = H[node2];
if (node2 < node1)
swap(node1, node2);
int lca = LCA(node1, node2, 1, size, 1).second;
lca = eulerArray[lca];
return level[prevn1] + level[prevn2] - 2 * level[lca];
}
int main() {
int N = 6;
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
FindNodeLevels(root);
createEulerTree(root);
creareEulerArray(2 * N - 1);
buildSegTree(1, 2 * N - 1, 1);
int Q = 4;
int query[Q][2] = {{1, 5}, {4, 6}, {3, 4}, {2, 4} };
for(int i = 0; i < Q; i++)
cout<<"The distance between two nodes of binary tree is "<<CalcNodeDistance(query[i][0], query[i][1], 2 * N - 1)<<endl;
return 0;
} আউটপুট
The distance between two nodes of binary tree is 2 The distance between two nodes of binary tree is 4 The distance between two nodes of binary tree is 3 The distance between two nodes of binary tree is 1


