মিন কস্ট পাথের জন্য পাইথন প্রোগ্রাম

এই নিবন্ধে, আমরা নীচে দেওয়া সমস্যার বিবৃতিটির সমাধান সম্পর্কে জানব৷

সমস্যা বিবৃতি − আমাদের একটি খরচ ম্যাট্রিক্স এবং একটি অবস্থান (m, n) দেওয়া হয়েছে, আমাদের (0, 0) থেকে (m, n) পৌঁছানোর জন্য সর্বনিম্ন খরচের পথের খরচ খুঁজে বের করতে হবে। প্রতিটি কোষ একটি কোষ থেকে অন্য কোষে যাওয়ার জন্য একটি খরচ উপস্থাপন করে৷

এখন নিচের বাস্তবায়নে সমাধানটি পর্যবেক্ষণ করা যাক -

উদাহরণ

# dynamic approach
R = 3
C = 3
def minCost(cost, m, n):
   # initialization
   tc = [[0 for x in range(C)] for x in range(R)]
   # base case
   tc[0][0] = cost[0][0]
   # total cost(tc) array
   for i in range(1, m + 1):
      tc[i][0] = tc[i-1][0] + cost[i][0]
   # tc array
   for j in range(1, n + 1):
      tc[0][j] = tc[0][j-1] + cost[0][j]
   # rest tc array
   for i in range(1, m + 1):
      for j in range(1, n + 1):
         tc[i][j] = min(tc[i-1][j-1], tc[i-1][j], tc[i][j-1]) + cost[i][j]
   return tc[m][n]
# main
cost = [[1, 5, 3],
        [7, 7, 4],
        [8, 5, 3]]
print("Total Cost:",minCost(cost, 2, 1))

আউটপুট

Total Cost: 13

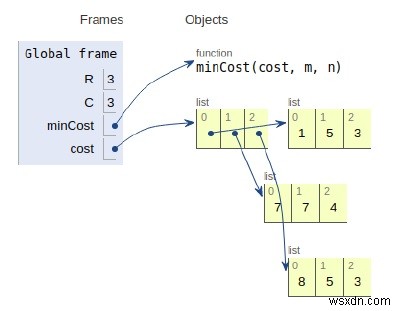
সমস্ত ভেরিয়েবল স্থানীয় সুযোগে ঘোষণা করা হয়েছে এবং তাদের উল্লেখ উপরের চিত্রে দেখা যাচ্ছে।

উপসংহার

এই প্রবন্ধে, আমরা শিখেছি কিভাবে আমরা মিন কস্ট পাথের জন্য একটি পাইথন প্রোগ্রাম তৈরি করতে পারি