গিথুবের সম্পূর্ণ উৎস
Stoffle প্রোগ্রামিং ভাষার একটি সম্পূর্ণ বাস্তবায়ন GitHub এ উপলব্ধ। এই রেফারেন্স বাস্তবায়ন কোড পড়া সহজ করতে সাহায্য করার জন্য অনেক মন্তব্য আছে. আপনি বাগ খুঁজে পেলে বা প্রশ্ন থাকলে নির্দ্বিধায় একটি সমস্যা খুলুন৷
এই ব্লগ পোস্টে, আমরা Stoffle-এর জন্য পার্সার প্রয়োগ করতে যাচ্ছি, একটি খেলনা প্রোগ্রামিং ভাষা যা সম্পূর্ণরূপে রুবিতে নির্মিত। আপনি এই সিরিজের প্রথম অংশে এই প্রকল্প সম্পর্কে আরও পড়তে পারেন।
স্ক্র্যাচ থেকে একটি পার্সার তৈরি করা আমাকে কিছু অপ্রত্যাশিত অন্তর্দৃষ্টি এবং জ্ঞান দিয়েছে। আমি অনুমান করি যে এই অভিজ্ঞতা ব্যক্তি থেকে ব্যক্তিতে পরিবর্তিত হতে পারে, তবে আমি মনে করি এটি অনুমান করা নিরাপদ যে এই নিবন্ধটির পরে, আপনি নিম্নলিখিতগুলির মধ্যে অন্তত একটি সম্পর্কে আপনার জ্ঞান অর্জন করেছেন বা আরও গভীর করেছেন:
- আপনি সোর্স কোড ভিন্নভাবে দেখতে শুরু করবেন এবং এর অনস্বীকার্য গাছের মতো গঠন লক্ষ্য করবেন অনেক সহজে;
- আপনার সিনট্যাকটিক সুগার সম্পর্কে গভীর ধারণা থাকবে এবং এটি সর্বত্র দেখা শুরু করবে, তা স্টফলে, রুবি বা এমনকি অন্যান্য প্রোগ্রামিং ভাষায়ই হোক।
আমি অনুভব করি যে একজন পার্সার প্যারেটো নীতির একটি নিখুঁত উদাহরণ। কিছু অতিরিক্ত-সুন্দর বৈশিষ্ট্য তৈরি করার জন্য যে পরিমান কাজের প্রয়োজন, যেমন দুর্দান্ত ত্রুটি বার্তা, তা স্পষ্টতই বেশি এবং বেসিকগুলি চালু করার জন্য প্রয়োজনীয় প্রচেষ্টার তুলনায় অসামঞ্জস্যপূর্ণ। আমার প্রিয় পাঠক, আমরা প্রয়োজনীয় বিষয়গুলির উপর ফোকাস করব এবং উন্নতিগুলিকে আপনার কাছে একটি চ্যালেঞ্জ হিসাবে ছেড়ে দেব। আমরা এই সিরিজের পরবর্তী নিবন্ধে আরও কিছু আকর্ষণীয় অতিরিক্ত কিছু পরিচালনা করতে পারি বা নাও করতে পারি।
সিনট্যাকটিক সুগার
সিনট্যাকটিক সুগার হল এমন একটি অভিব্যক্তি যা এমন গঠন বোঝাতে ব্যবহৃত হয় যা একটি ভাষাকে ব্যবহার করা সহজ করে তোলে, কিন্তু যেটির অপসারণের ফলে প্রোগ্রামিং ভাষা কার্যকারিতা হারাতে পারে না। একটি চমৎকার উদাহরণ হল রুবির
elsifনির্মাণ স্টফলে, আমাদের এমন একটি কাঠামো নেই, তাই এটি প্রকাশ করার জন্য আমরা আরও শব্দযুক্ত হতে বাধ্য হই:if some_condition # ... else # oops, no elsif available if another_condition # ... end end
পার্সার কি?
আমরা সোর্স কোড দিয়ে শুরু করি, অক্ষরের একটি কাঁচা ক্রম। তারপর, এই সিরিজের পূর্ববর্তী নিবন্ধে দেখানো হয়েছে, লেক্সার এই অক্ষরগুলিকে টোকেন নামক সংবেদনশীল ডেটা স্ট্রাকচারে গ্রুপ করে। যাইহোক, আমাদের কাছে এখনও এমন ডেটা বাকি রয়েছে যা সম্পূর্ণ সমতল, এমন কিছু যা এখনও সোর্স কোডের নেস্টেড প্রকৃতিকে যথাযথভাবে উপস্থাপন করে না। এইভাবে, পার্সারের অক্ষরের এই ক্রম থেকে একটি গাছ তৈরি করার কাজ রয়েছে। যখন এটি তার কাজ শেষ করে, তখন আমরা এমন ডেটা দিয়ে শেষ করব যা শেষ পর্যন্ত প্রকাশ করতে সক্ষম হয় যে কীভাবে আমাদের প্রোগ্রামের প্রতিটি অংশ একে অপরের সাথে বাসা বাঁধে এবং একে অপরের সাথে সম্পর্কিত।
পার্সার দ্বারা তৈরি করা গাছটিকে সাধারণত বিমূর্ত সিনট্যাক্স ট্রি (AST) বলা হয়। নাম থেকেই বোঝা যাচ্ছে, আমরা একটি ট্রি ডাটা স্ট্রাকচার নিয়ে কাজ করছি, যার রুট প্রোগ্রাম নিজেই প্রতিনিধিত্ব করে এবং এই প্রোগ্রাম নোডের বাচ্চারা আমাদের প্রোগ্রাম তৈরি করে এমন অনেক এক্সপ্রেশন। শব্দটি বিমূর্ত AST-এ আমাদের বিমূর্ততা করার ক্ষমতা বোঝায় যে অংশগুলি, পূর্ববর্তী ধাপে, স্পষ্টভাবে উপস্থিত ছিল। একটি ভাল উদাহরণ হল এক্সপ্রেশন টার্মিনেটর (স্টফলের ক্ষেত্রে নতুন লাইন); এএসটি তৈরি করার সময় এগুলি বিবেচনা করা হয়, তবে একটি টার্মিনেটরকে উপস্থাপন করার জন্য আমাদের একটি নির্দিষ্ট নোডের প্রয়োজন নেই। যাইহোক, মনে রাখবেন, আমাদের কাছে একটি স্পষ্ট টোকেন ছিল একটি টার্মিনেটর প্রতিনিধিত্ব করতে।
এটি একটি উদাহরণ AST একটি ভিজ্যুয়ালাইজেশন আছে দরকারী হবে না? আপনার ইচ্ছা একটি আদেশ! নীচে একটি সাধারণ Stoffle প্রোগ্রাম, যা আমরা এই পোস্টে ধাপে ধাপে বিশ্লেষণ করব, এবং এর সংশ্লিষ্ট বিমূর্ত সিনট্যাক্স ট্রি:
fn double: num
num * 2
end
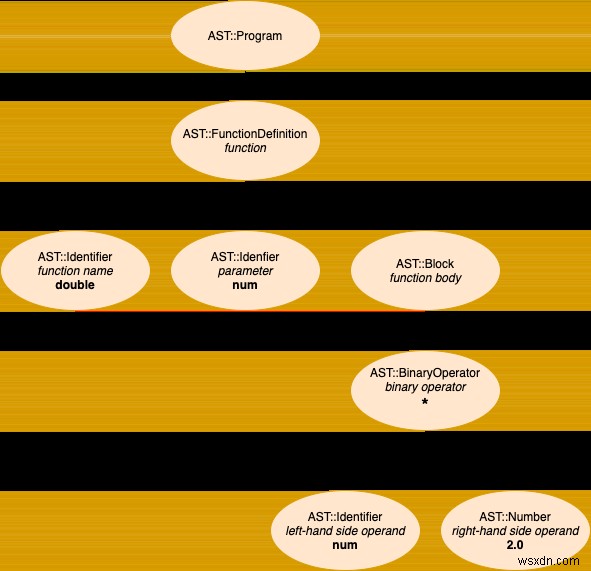
উৎস থেকে AST পর্যন্ত, একটি প্রথম উদাহরণ
পোস্টের এই বিভাগে, আমরা ধাপে ধাপে অন্বেষণ করতে যাচ্ছি, কিভাবে আমাদের পার্সার একটি খুব পরিচালনা করে সাধারণ Stoffle প্রোগ্রাম, একটি একক লাইনের সমন্বয়ে গঠিত যেখানে একটি ভেরিয়েবল বাইন্ডিং প্রকাশ করা হয় (অর্থাৎ, আমরা একটি ভেরিয়েবলের জন্য একটি মান নির্ধারণ করি)। এখানে উৎস হল, লেক্সার দ্বারা উত্পাদিত টোকেনগুলির একটি সরলীকৃত উপস্থাপনা (এই টোকেনগুলি আমাদের পার্সারকে দেওয়া ইনপুট) এবং অবশেষে, প্রোগ্রামটি উপস্থাপন করার জন্য আমরা যে AST তৈরি করতে যাচ্ছি তার একটি ভিজ্যুয়াল উপস্থাপনা:
উৎস
my_var = 1
টোকেন (লেক্সারের আউটপুট, পার্সারের জন্য ইনপুট)
[:identifier, :'=', :number]
পার্সারের আউটপুটের ভিজ্যুয়াল রিপ্রেজেন্টেশন (একটি বিমূর্ত সিনট্যাক্স ট্রি)
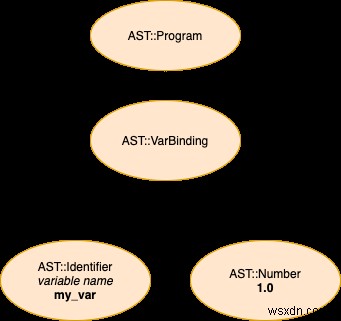
আপনি কল্পনা করতে পারেন, আমাদের পার্সারের মূলটি আমাদের লেক্সারের মূলের সাথে খুব মিল। লেক্সারের ক্ষেত্রে, প্রক্রিয়া করার জন্য আমাদের কাছে একগুচ্ছ অক্ষর ছিল। এখন, আমাদের এখনও একটি সংগ্রহের উপর পুনরাবৃত্তি করতে হবে, কিন্তু পার্সারের ক্ষেত্রে, আমরা আমাদের লেক্সার বন্ধু দ্বারা উত্পাদিত টোকেনগুলির তালিকার উপরে যাব। আমাদের একটি একক পয়েন্টার আছে (@next_p ) টোকেন সংগ্রহে আমাদের অবস্থানের উপর নজর রাখতে। এই পয়েন্টারটি পরবর্তী চিহ্নিত করে টোকেন প্রক্রিয়া করা হবে। যদিও আমাদের কাছে শুধুমাত্র এই একক পয়েন্টার আছে, আমাদের কাছে আরও অনেক "ভার্চুয়াল" পয়েন্টার রয়েছে যা আমরা প্রয়োজন অনুসারে ব্যবহার করতে পারি; আমরা বাস্তবায়ন বরাবর এগিয়ে তারা প্রদর্শিত হবে. এরকম একটি "ভার্চুয়াল" পয়েন্টার হল বর্তমান (মূলত, @next_p - 1-এ টোকেন )।
#পার্স টোকেনগুলিকে AST-এ রূপান্তরিত করার জন্য কল করার পদ্ধতি হল, যা @ast-এ উপলব্ধ হবে উদাহরণস্বরূপ পরিবর্তনশীল. #parse এর বাস্তবায়ন সোজা। আমরা #consume কল করে সংগ্রহের মাধ্যমে অগ্রসর হতে থাকি এবং @next_p সরানো হচ্ছে যতক্ষণ না প্রক্রিয়া করার জন্য আর কোন টোকেন না থাকে (অর্থাৎ, যখন next_p #parse_expr_recursively একটি AST নোড বা কিছুই ফেরত দিতে পারে; মনে রাখবেন, আমাদের AST-তে টার্মিনেটরদের প্রতিনিধিত্ব করার দরকার নেই, উদাহরণস্বরূপ। যদি লুপের বর্তমান পুনরাবৃত্তিতে একটি নোড তৈরি করা হয় তবে আমরা এটিকে @ast এ যোগ করি চালিয়ে যাওয়ার আগে। এটা মনে রাখা গুরুত্বপূর্ণ যে #parse_expr_recursively এছাড়াও @next_p সরানো হচ্ছে যেহেতু, যখন আমরা একটি টোকেন খুঁজে পাই যা একটি নির্দিষ্ট নির্মাণের সূচনা চিহ্নিত করে, তখন আমাদের একাধিকবার অগ্রসর হতে হবে যতক্ষণ না আমরা একটি নোড তৈরি করতে সক্ষম হই যা আমরা বর্তমানে পার্স করছি। একটি if প্রতিনিধিত্ব করে একটি নোড তৈরি করতে আমাদের কতগুলি টোকেন ব্যবহার করতে হবে তা কল্পনা করুন .
module Stoffle
class Parser
attr_accessor :tokens, :ast, :errors
# ...
def initialize(tokens)
@tokens = tokens
@ast = AST::Program.new
@next_p = 0
@errors = []
end
def parse
while pending_tokens?
consume
node = parse_expr_recursively
ast << node if node != nil
end
end
# ...
end
end
উপরের স্নিপেটে, প্রথমবারের মতো, আমাদের পার্সার বাস্তবায়নের অংশ এমন অনেক ধরনের AST নোডের মধ্যে একটি উপস্থাপন করা হয়েছে। নীচে, আমাদের কাছে AST::Program এর জন্য সম্পূর্ণ সোর্স কোড রয়েছে নোড টাইপ। আপনি অনুমান করতে পারেন, এটি আমাদের গাছের মূল, পুরো প্রোগ্রামের প্রতিনিধিত্ব করে। আসুন এটির সবচেয়ে আকর্ষণীয় বিটগুলি ঘনিষ্ঠভাবে দেখে নেওয়া যাক:
- একটি স্টফল প্রোগ্রাম
@expressionsদ্বারা গঠিত; এই হল#শিশুএকটিAST::প্রোগ্রামএর নোড; - যেমন আপনি আবার দেখতে পাবেন, প্রতিটি নোড প্রকার
#==প্রয়োগ করে পদ্ধতি ফলস্বরূপ, দুটি সাধারণ নোডের পাশাপাশি সম্পূর্ণ প্রোগ্রামগুলির তুলনা করা সহজ! দুটি প্রোগ্রাম (বা দুটি জটিল নোড) তুলনা করার সময়, তাদের সমতা প্রতিটি শিশুর সমতা, প্রতিটি শিশুর প্রতিটি শিশুর সমতা ইত্যাদি দ্বারা নির্ধারিত হবে। এই সহজ অথচ শক্তিশালী কৌশলটি#==ব্যবহার করেছে আমাদের বাস্তবায়ন পরীক্ষা করার জন্য অত্যন্ত দরকারী৷
class Stoffle::AST::Program
attr_accessor :expressions
def initialize
@expressions = []
end
def <<(expr)
expressions << expr
end
def ==(other)
expressions == other&.expressions
end
def children
expressions
end
end
অভিব্যক্তি বনাম বিবৃতি
কিছু ভাষায়, অনেক নির্মাণ একটি মান তৈরি করে না; একটি শর্তাধীন একটি ক্লাসিক উদাহরণ। এগুলোকে বিবৃতি বলা হয় . অন্যান্য নির্মাণ, যাইহোক, একটি মান মূল্যায়ন করে (যেমন, একটি ফাংশন কল)। এগুলোকে অভিব্যক্তি বলা হয় . অন্যান্য ভাষায়, যাইহোক, সবকিছুই একটি অভিব্যক্তি এবং একটি মান তৈরি করে। রুবি এই পদ্ধতির একটি উদাহরণ। উদাহরণ স্বরূপ, একটি পদ্ধতির সংজ্ঞা কোন মূল্যকে মূল্যায়ন করে তা খুঁজে বের করতে IRB-তে নিম্নলিখিত স্নিপেটটি টাইপ করার চেষ্টা করুন:
irb(main):001:0> def two; 2; endআপনি যদি IRB-কে বরখাস্ত করার মত অনুভব না করেন, তাহলে আমাকে আপনার কাছে খবরটি জানাতে দিন; রুবিতে, একটি পদ্ধতির সংজ্ঞা অভিব্যক্তি একটি প্রতীক (পদ্ধতির নাম) মূল্যায়ন করে। যেমন আপনি জানেন, Stoffle রুবিতে ব্যাপকভাবে অনুপ্রাণিত, তাই আমাদের ছোট্ট খেলনা ভাষায়, সবকিছুই একটি অভিব্যক্তি।
মনে রাখবেন যে এই সংজ্ঞাগুলি ব্যবহারিক উদ্দেশ্যে যথেষ্ট ভাল, কিন্তু প্রকৃতপক্ষে একটি সম্মতি নেই, এবং আপনি দেখতে পারেন যে পদের বিবৃতি এবং অভিব্যক্তি অন্য কোথাও ভিন্নভাবে সংজ্ঞায়িত করা হচ্ছে৷
ডিপার ডাইভিং:#parse_expr_recursively বাস্তবায়ন শুরু করা
আমরা উপরের স্নিপেটে যেমন দেখেছি, #parse_expr_recursively সম্ভাব্য একটি নতুন AST নোড তৈরি করতে বলা পদ্ধতি। #parse_expr_recursively পার্সিং প্রক্রিয়ায় অন্যান্য ছোট পদ্ধতির আধিক্য ব্যবহার করে, কিন্তু আমরা প্রশান্তির সাথে বলতে পারি যে এটি আমাদের পার্সারের আসল ইঞ্জিন। যদিও এটি খুব দীর্ঘ নয়, এই পদ্ধতিটি হজম করা আরও কঠিন। অতএব, আমরা এটি দুটি অংশে কাটা যাচ্ছি। পোস্টের এই বিভাগে, এর প্রাথমিক সেগমেন্ট দিয়ে শুরু করা যাক, যা ইতিমধ্যেই যথেষ্ট শক্তিশালী Stoffle প্রোগ্রামিং ভাষার কিছু সহজ অংশ পার্স করার জন্য। একটি রিফ্রেসার হিসাবে, মনে রাখবেন যে আমরা একটি একক পরিবর্তনশীল বাইন্ডিং এক্সপ্রেশন সমন্বিত একটি সাধারণ প্রোগ্রাম পার্স করার জন্য প্রয়োজনীয় পদক্ষেপগুলি অতিক্রম করছি:
উৎস
my_var = 1
টোকেন (লেক্সারের আউটপুট, পার্সারের জন্য ইনপুট)
[:identifier, :'=', :number]
টোকেনগুলি দেখার পরে আমাদেরকে মোকাবেলা করতে হবে এবং অন্যান্য, অনুরূপ সাধারণ অভিব্যক্তিগুলির জন্য লেক্সার আউটপুট কী হবে তা কল্পনা করার পরে, নির্দিষ্ট পার্সিং পদ্ধতির সাথে টোকেন প্রকারগুলিকে সংযুক্ত করার চেষ্টা করা একটি ভাল ধারণা বলে মনে হচ্ছে:
def parse_expr_recursively
parsing_function = determine_parsing_function
if parsing_function.nil?
unrecognized_token_error
return
end
send(parsing_function)
end
এই প্রাথমিক বাস্তবায়নে #parse_expr_recursively , যে আমরা ঠিক কি. যেহেতু বেশ অনেক থাকবে বিভিন্ন ধরনের টোকেন আমাদের পরিচালনা করতে হবে, এই সিদ্ধান্ত নেওয়ার প্রক্রিয়াটিকে একটি পৃথক পদ্ধতিতে বের করা ভাল -#determine_parsing_function , যা আমরা কিছুক্ষণের মধ্যে দেখতে পাব৷
আমরা শেষ হয়ে গেলে, এমন কোনো টোকেন থাকা উচিত নয় যা আমরা চিনতে পারি না, তবে সুরক্ষা হিসাবে, বর্তমান টোকেনের সাথে একটি পার্সিং ফাংশন যুক্ত কিনা তা আমরা পরীক্ষা করব। যদি তা না হয়, আমরা আমাদের ইনস্ট্যান্স ভেরিয়েবল @errors এ একটি ত্রুটি যোগ করব , যা পার্সিংয়ের সময় ঘটে যাওয়া সমস্ত সমস্যা ধারণ করে। আমরা এখানে বিস্তারিতভাবে এটি কভার করব না, তবে আপনি যদি কৌতূহলী হন তবে আপনি GitHub-এ পার্সারের সম্পূর্ণ বাস্তবায়ন পরীক্ষা করতে পারেন৷
#determine_parsing_function পার্সিং পদ্ধতির নামের প্রতিনিধিত্বকারী একটি চিহ্ন প্রদান করে যা কল করা হবে। আমরা রুবির send ব্যবহার করব ফ্লাইতে উপযুক্ত পদ্ধতিতে কল করতে।
পার্সিং পদ্ধতি নির্ধারণ করা এবং একটি পরিবর্তনশীল বাইন্ডিং পার্স করা
এর পরে, চলুন #determine_parsing_function দেখে নেওয়া যাক Stoffle এর বিভিন্ন গঠন পার্স করার জন্য নির্দিষ্ট পদ্ধতি কল করার এই প্রাথমিক প্রক্রিয়াটি বুঝতে। #determine_parsing_function বাইনারি অপারেটর ছাড়া সবকিছুর জন্য (যেমন, কীওয়ার্ড এবং ইউনারী অপারেটর) ব্যবহার করা হবে। আমরা পরে বাইনারি অপারেটরদের ক্ষেত্রে ব্যবহৃত কৌশলটি অন্বেষণ করব। আপাতত, আসুন #determine_parsing_function চেক আউট করি :
def determine_parsing_function
if [:return, :identifier, :number, :string, :true, :false, :nil, :fn,
:if, :while].include?(current.type)
"parse_#{current.type}".to_sym
elsif current.type == :'('
:parse_grouped_expr
elsif [:"\n", :eof].include?(current.type)
:parse_terminator
elsif UNARY_OPERATORS.include?(current.type)
:parse_unary_operator
end
end
যেমন আগে ব্যাখ্যা করা হয়েছে, #current একটি ভার্চুয়াল এই মুহুর্তে প্রক্রিয়া করা হচ্ছে টোকেন নির্দেশক. #determine_parsing_function এর বাস্তবায়ন খুব সোজা; আমরা বর্তমান টোকেন দেখি (বিশেষ করে, এর টাইপ ) এবং কল করার উপযুক্ত পদ্ধতির প্রতিনিধিত্ব করে একটি প্রতীক ফেরত দিন।
মনে রাখবেন যে আমরা একটি ভেরিয়েবল বাইন্ডিং পার্স করার জন্য প্রয়োজনীয় পদক্ষেপগুলি অতিক্রম করছি (my_var =1 ), তাই আমরা যে টোকেন প্রকারগুলি পরিচালনা করছি তা হল [:identifier, :'=', :number] . বর্তমান টোকেনের ধরন হল :identifier , তাই #determine_parsing_function :parse_identifier ফেরত দেবে , আপনি অনুমান করা হতে পারে. আসুন আমাদের পরবর্তী ধাপে এক নজরে দেখি, #parse_identifier পদ্ধতি:
def parse_identifier
lookahead.type == :'=' ? parse_var_binding : AST::Identifier.new(current.lexeme)
end
এখানে, আমাদের কাছে একটি খুব সহজ প্রকাশ রয়েছে, মূলত, অন্যান্য সমস্ত পার্স পদ্ধতিগুলি কী করে। #parse_identifier-এ - এবং অন্যান্য পার্স পদ্ধতিতে - আমরা যে কাঠামোটি আশা করছি তা আসলে উপস্থিত কিনা তা নির্ধারণ করতে আমরা টোকেনগুলি পরীক্ষা করি। আমরা জানি আমাদের একটি শনাক্তকারী আছে, কিন্তু আমরা একটি ভেরিয়েবল বাইন্ডিং নিয়ে কাজ করছি কিনা তা নির্ধারণ করার জন্য আমাদের পরবর্তী টোকেনটি দেখতে হবে, যা পরবর্তী টোকেন প্রকার :'=' হলে তা হবে। , অথবা যদি আমাদের নিজের দ্বারা একটি শনাক্তকারী থাকে বা আরও জটিল অভিব্যক্তিতে অংশগ্রহণ করে। কল্পনা করুন, উদাহরণস্বরূপ, একটি গাণিতিক অভিব্যক্তি যেখানে আমরা ভেরিয়েবলে সংরক্ষিত মানগুলিকে হেরফের করছি৷
যেহেতু আমাদের কাছে একটি :'=' আছে পরবর্তীতে আসছে, #parse_var_binding বলা হবে:
def parse_var_binding
identifier = AST::Identifier.new(current.lexeme)
consume(2)
AST::VarBinding.new(identifier, parse_expr_recursively)
end
এখানে, আমরা বর্তমানে যে শনাক্তকারীকে প্রক্রিয়া করছি তার প্রতিনিধিত্ব করতে একটি নতুন AST নোড তৈরি করে শুরু করি। AST::Identifier-এর কনস্ট্রাক্টর শনাক্তকারী টোকেনের লেক্সেম আশা করে (যেমন, অক্ষরের ক্রম, স্ট্রিং "my_var" আমাদের ক্ষেত্রে), তাই আমরা এটি সরবরাহ করি। তারপরে আমরা প্রক্রিয়াকরণের অধীনে টোকেনগুলির স্রোতে দুটি স্থান অগ্রসর করি, টাইপ :number সহ টোকেন তৈরি করি। পরেরটি বিশ্লেষণ করা হবে। মনে রাখবেন যে আমরা [:identifier, :'=', :number] নিয়ে কাজ করছি .
অবশেষে, আমরা ভেরিয়েবল বাইন্ডিং প্রতিনিধিত্ব করে একটি AST নোড তৈরি করে ফেরত দিই। AST::VarBinding-এর কনস্ট্রাক্টর দুটি পরামিতি আশা করে:একটি শনাক্তকারী AST নোড (বাইন্ডিং এক্সপ্রেশনের বাম দিকে) এবং কোনো বৈধ অভিব্যক্তি (ডান দিকে)। এখানে উল্লেখ্য একটি গুরুত্বপূর্ণ বিষয় আছে; ভেরিয়েবল বাইন্ডিং এক্সপ্রেশনের ডানদিকে তৈরি করতে, আমরা কল করি #parse_expr_recursively আবার . এটি প্রথমে কিছুটা অদ্ভুত মনে হতে পারে, তবে মনে রাখবেন যে একটি পরিবর্তনশীল একটি খুব জটিল অভিব্যক্তিতে আবদ্ধ হতে পারে, কেবলমাত্র একটি সংখ্যার সাথে নয়, যেমনটি আমাদের উদাহরণের ক্ষেত্রে। আমরা যদি আমাদের পার্সিং কৌশলকে এক কথায় সংজ্ঞায়িত করি, তাহলে তা হবে পুনরাবৃত্ত . এখন, আমার ধারণা আপনি বুঝতে শুরু করেছেন কেন #parse_expr_recursively এর নাম আছে।
আমরা এই বিভাগটি শেষ করার আগে, আমাদের দ্রুত AST::Identifier উভয়ই অন্বেষণ করা উচিত এবং AST::VarBinding . প্রথমে, AST::Identifier :
class Stoffle::AST::Identifier < Stoffle::AST::Expression
attr_accessor :name
def initialize(name)
@name = name
end
def ==(other)
name == other&.name
end
def children
[]
end
end
এখানে অভিনব কিছু নেই। এটা উল্লেখ করার মতো যে নোড ভেরিয়েবলের নাম সংরক্ষণ করে এবং এর বাচ্চা নেই।
এখন, AST::VarBinding :
class Stoffle::AST::VarBinding < Stoffle::AST::Expression
attr_accessor :left, :right
def initialize(left, right)
@left = left
@right = right
end
def ==(other)
children == other&.children
end
def children
[left, right]
end
end
বাম দিকে একটি AST::সনাক্তকারী নোড ডানদিকের দিকটি প্রায় প্রতিটি সম্ভাব্য ধরণের নোড - একটি সাধারণ সংখ্যা থেকে, যেমন আমাদের উদাহরণে, আরও জটিল কিছু - অভিব্যক্তিটি উপস্থাপন করে যার সাথে শনাক্তকারী আবদ্ধ। #শিশু একটি পরিবর্তনশীল বাইন্ডিং হল AST নোড যা এটি @left এ ধারণ করে এবং @right .
উৎস থেকে AST পর্যন্ত, একটি দ্বিতীয় উদাহরণ
#parse_expr_recursively এর বর্তমান অবতার ইতিমধ্যেই কিছু সাধারণ অভিব্যক্তি পার্স করতে সক্ষম, যেমনটি আমরা পূর্ববর্তী বিভাগে দেখেছি। এই বিভাগে, আমরা এটির বাস্তবায়ন শেষ করব যাতে এটি আরও জটিল সত্তা যেমন বাইনারি এবং লজিক্যাল অপারেটরকে পার্স করতে সক্ষম হয়। এখানে, আমরা ধাপে ধাপে অন্বেষণ করব, কীভাবে আমাদের পার্সার একটি ফাংশন সংজ্ঞায়িত করে এমন একটি প্রোগ্রাম পরিচালনা করে। এখানে উৎস, লেক্সার দ্বারা উত্পাদিত টোকেনগুলির একটি সরলীকৃত উপস্থাপনা এবং, যেমনটি আমরা প্রথম বিভাগে পেয়েছি, AST-এর একটি ভিজ্যুয়াল উপস্থাপনা যা আমরা প্রোগ্রামটি উপস্থাপন করার জন্য তৈরি করব:
উৎস
fn double: num
num * 2
end
টোকেন (লেক্সারের আউটপুট, পার্সারের জন্য ইনপুট)
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
পার্সারের আউটপুটের ভিজ্যুয়াল রিপ্রেজেন্টেশন (একটি বিমূর্ত সিনট্যাক্স ট্রি)

আমরা এগিয়ে যাওয়ার আগে, আসুন একধাপ পিছিয়ে যাই এবং অপারেটর অগ্রাধিকার নিয়ম সম্পর্কে কথা বলি। এগুলি গাণিতিক নিয়মের উপর ভিত্তি করে; গণিতে, এগুলি কেবলমাত্র নিয়মাবলী, এবং প্রকৃতপক্ষে, আমরা যে অপারেটর প্রাধান্যের সাথে অভ্যস্ত, সেখানে মৌলিক কিছু নেই। এই নিয়মগুলি আমাদেরকে একটি অভিব্যক্তি মূল্যায়নের জন্য সঠিক ক্রম নির্ধারণ করার অনুমতি দেয় এবং, আমাদের ক্ষেত্রে, প্রথমে এটি পার্স করার জন্য। প্রতিটি অপারেটরের অগ্রাধিকার সংজ্ঞায়িত করার জন্য, আমাদের কাছে কেবল একটি মানচিত্র রয়েছে (যেমন, একটি হ্যাশ ) টোকেন প্রকার এবং পূর্ণসংখ্যা। উচ্চতর সংখ্যা মানে একজন অপারেটরকে প্রথম পরিচালনা করা উচিত :
# We define these precedence rules at the top of Stoffle::Parser.
module Stoffle
class Parser
# ...
UNARY_OPERATORS = [:'!', :'-'].freeze
BINARY_OPERATORS = [:'+', :'-', :'*', :'/', :'==', :'!=', :'>', :'<', :'>=', :'<='].freeze
LOGICAL_OPERATORS = [:or, :and].freeze
LOWEST_PRECEDENCE = 0
PREFIX_PRECEDENCE = 7
OPERATOR_PRECEDENCE = {
or: 1,
and: 2,
'==': 3,
'!=': 3,
'>': 4,
'<': 4,
'>=': 4,
'<=': 4,
'+': 5,
'-': 5,
'*': 6,
'/': 6,
'(': 8
}.freeze
# ...
end
end
#parse_expr_recursively-এ ব্যবহৃত কৌশল কম্পিউটার বিজ্ঞানী ভন প্র্যাট তার 1973 সালের গবেষণাপত্র "টপ ডাউন অপারেটর প্রিসিডেন্স"-এ উপস্থাপিত বিখ্যাত পার্সার অ্যালগরিদমের উপর ভিত্তি করে তৈরি। আপনি দেখতে পাবেন, অ্যালগরিদম খুব সহজ, কিন্তু সম্পূর্ণরূপে উপলব্ধি করা একটু কঠিন। কেউ বলতে পারে যে এটি কিছুটা জাদুকর মনে হয়। এই কৌশলটির কার্যকারিতা সম্পর্কে একটি স্বজ্ঞাত বোঝার চেষ্টা করার জন্য আমরা এই পোস্টে যা করব তা হল ধাপে ধাপে, উপরে উল্লিখিত স্টফল স্নিপেটটি পার্স করার সাথে সাথে কী ঘটে। তাই, আর কোনো ঝামেলা ছাড়াই, এখানে #parse_expr_recursively-এর সম্পূর্ণ সংস্করণ দেওয়া হল :
def parse_expr_recursively(precedence = LOWEST_PRECEDENCE)
parsing_function = determine_parsing_function
if parsing_function.nil?
unrecognized_token_error
return
end
expr = send(parsing_function)
return if expr.nil? # When expr is nil, it means we have reached a \n or a eof.
# Note that, here, we are checking the NEXT token.
while nxt_not_terminator? && precedence < nxt_precedence
infix_parsing_function = determine_infix_function(nxt)
return expr if infix_parsing_function.nil?
consume
expr = send(infix_parsing_function, expr)
end
expr
end
#parse_expr_recursively এখন একটি প্যারামিটার গ্রহণ করে, অগ্রাধিকার . এটি পদ্ধতির একটি প্রদত্ত কলে বিবেচনা করা অগ্রাধিকার "স্তর" প্রতিনিধিত্ব করে। উপরন্তু, পদ্ধতির প্রথম অংশটি প্রায় একই রকম। তারপর - যদি আমরা এই প্রথম অংশে একটি অভিব্যক্তি তৈরি করতে সক্ষম হই - তবে পদ্ধতির অভিনব অংশটি আসে। যদিও পরবর্তী টোকেনটি টার্মিনেটর নয় (যেমন, একটি লাইন বিরতি বা ফাইলের শেষ) এবং অগ্রাধিকার (অগ্রাধিকার param) পরবর্তী টোকেনের অগ্রাধিকারের চেয়ে কম, আমরা সম্ভাব্যভাবে টোকেন স্ট্রীম ব্যবহার করা চালিয়ে যাচ্ছি।
ভিতরে দেখার আগে যখন , আসুন এর দ্বিতীয় শর্তের অর্থ সম্পর্কে একটু চিন্তা করি (precedence expr স্থানীয় পরিবর্তনশীল) সম্ভবত একটি নোডের একটি শিশু যা এখনও তৈরি করা হয়নি (মনে রাখবেন যে আমরা একটি AST তৈরি করছি, একটি বিমূর্ত সিনট্যাক্স ট্রি ) আমাদের স্টফল স্নিপেটের পার্সিংয়ের মধ্য দিয়ে যাওয়ার আগে, আসুন একটি সাধারণ গাণিতিক অভিব্যক্তির পার্সিং সম্পর্কে চিন্তা করি:2 + 2 . এই অভিব্যক্তিটি পার্স করার সময়, আমাদের পদ্ধতির প্রথম অংশটি একটি AST::Number তৈরি করবে প্রথম 2 প্রতিনিধিত্বকারী নোড এবং এটি expr এ সংরক্ষণ করুন . তারপর, আমরা যখন-এ পা রাখব কারণ পরবর্তী টোকেনের অগ্রাধিকার (:'+' ) ডিফল্ট অগ্রাধিকারের চেয়ে বেশি হবে। তারপরে আমাদের কাছে পার্সিং পদ্ধতি থাকবে যার নাম একটি যোগফল পরিচালনা করার জন্য, এটিকে AST::Number পাস করে। নোড এবং একটি বাইনারি অপারেটর প্রতিনিধিত্বকারী একটি নোড রিসিভিং (AST::BinaryOperator ) অবশেষে, আমরা ওভাররাইট করব expr-এ সংরক্ষিত মান , প্রথম 2 প্রতিনিধিত্বকারী নোড 2 + 2-এ , প্লাস অপারেটর প্রতিনিধিত্ব করে এই নতুন নোডের সাথে। লক্ষ্য করুন যে শেষ পর্যন্ত, এই অ্যালগরিদম আমাদের নোডগুলিকে পুনরায় সাজানোর অনুমতি দিয়েছে; আমরা AST::Number তৈরি করে শুরু করেছি নোড এবং AST::BinaryOperator-এর সন্তানদের একজন হিসাবে এটি আমাদের গাছের একটি গভীর নোড হিসাবে শেষ হয়েছে। নোড।
একটি ফাংশনের সংজ্ঞা ধাপে ধাপে পার্স করা
এখন যেহেতু আমরা #parse_expr_recursively এর সামগ্রিক ব্যাখ্যা দিয়েছি , আসুন আমাদের সাধারণ ফাংশনের সংজ্ঞায় ফিরে আসি:
fn double: num
num * 2
end
এমনকি এই স্নিপেটটি পার্স করার সময় পার্সার এক্সিকিউশনের একটি সরলীকৃত বর্ণনার দিকে নজর দেওয়ার ধারণাটি ক্লান্তিকর মনে হতে পারে (এবং, প্রকৃতপক্ষে, সম্ভবত এটি!), কিন্তু আমি মনে করি এটি #parse_expr_recursively<উভয়কে আরও ভালভাবে বোঝার জন্য খুবই মূল্যবান। /কোড> এবং নির্দিষ্ট বিটের পার্সিং (ফাংশনের সংজ্ঞা এবং পণ্য অপারেটর)। প্রথম জিনিসগুলি প্রথমে, এখানে টোকেন প্রকারগুলি রয়েছে যা আমরা নিয়ে কাজ করব (নীচে @tokens.map(&:type) এর আউটপুট রয়েছে , লেক্সার স্নিপেটটিকে টোকেনাইজ করা শেষ করার পরে পার্সারের ভিতরে আমরা এইমাত্র দেখেছি):
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
নীচের সারণীটি দেখায় যে ক্রম অনুসারে আমরা উপরের টোকেনগুলিকে পার্স করে সবচেয়ে গুরুত্বপূর্ণ পদ্ধতিগুলিকে বলা হয়৷ মনে রাখবেন যে এটি একটি সরলীকরণ, এবং আপনি যদি পার্সার সম্পাদনের সমস্ত সঠিক পদক্ষেপগুলি সত্যিই বুঝতে চান তবে আমি একটি রুবি ডিবাগার ব্যবহার করার পরামর্শ দিচ্ছি, যেমন বাইবাগ, এবং প্রোগ্রামটি চালানোর সাথে সাথে লাইন-বাই-লাইন অগ্রিম। পি>
অণুবীক্ষণ যন্ত্রের অধীনে আমাদের পার্সার
একটি পরীক্ষা আছে যা এই সঠিক স্নিপেটটি ব্যবহার করে যা আমরা অন্বেষণ করছি, যা Stoffle এর উৎসে পাওয়া যায়। আপনি এটি spec/lib/stoffle/parser_spec.rb এর ভিতরে খুঁজে পেতে পারেন; এটি সেই পরীক্ষা যা
complex_program_ok_2.sfeনামক স্নিপেট ব্যবহার করে .ধাপে ধাপে পার্সার এক্সিকিউশন অন্বেষণ করতে, আপনি উৎস সম্পাদনা করতে পারেন এবং
byebug-এ একটি কল যোগ করতে পারেনপার্সার#পার্সএর শুরুতে , RSpec দিয়ে শুধুমাত্র পূর্বোক্ত পরীক্ষা চালান এবং তারপর Byebug এরstepব্যবহার করুন একটি সময়ে একটি লাইন প্রোগ্রাম অগ্রসর করার জন্য কমান্ড.GitHub এ প্রজেক্টের README ফাইলে গিয়ে Byebug কীভাবে কাজ করে এবং সমস্ত উপলব্ধ কমান্ডগুলি সম্পর্কে আরও তথ্য দেখুন৷
| কথিত পদ্ধতি | বর্তমান টোকেন | পরবর্তী টোকেন | উল্লেখযোগ্য ভেরিয়েবল / কল ফলাফল | Obs |
|---|---|---|---|---|
| পার্স করুন | শূন্য | :fn | ||
| parse_expr_recursively | :fn | :identifier | অগ্রসরতা =0, পার্সিং_ফাংশন =:পার্স_এফএন | |
| পার্স_ফাংশন_ডেফিনিশন | :fn | :identifier | parse_fn হল parse_function_definition এর একটি উপনাম | |
| parse_function_params | :identifier | :":" | ||
| পার্স_ব্লক | :"\n" | :identifier | ||
| parse_expr_recursively | :identifier | :* | precedence =0, parsing_function =:parse_identifier, nxt_precedence() রিটার্ন 6, infix_parsing_function =:parse_binary_operator | |
| পার্স_আইডেন্টিফায়ার | :identifier | :* | ||
| parse_binary_operator | :* | :number | op_precedence =6 | |
| parse_expr_recursively | :number | :"\n" | precedence =6, parsing_function =:parse_number, nxt_precedence() রিটার্ন 0 | |
| পার্স_সংখ্যা | :number | :"\n" |
এখন যেহেতু আমাদের একটি সাধারণ ধারণা রয়েছে যে কোন পদ্ধতিগুলিকে বলা হয়, সেইসাথে ক্রম, আসুন কিছু পার্সিং পদ্ধতি অধ্যয়ন করি যা আমরা এখনও বিশদভাবে দেখিনি৷
#পার্স_ফাংশন_ডেফিনিশন পদ্ধতি
পদ্ধতি #parse_function_definition কল করা হয়েছিল যখন বর্তমান টোকেনটি ছিল :fn এবং পরেরটি ছিল :identifier :
def parse_function_definition
return unless consume_if_nxt_is(build_token(:identifier))
fn = AST::FunctionDefinition.new(AST::Identifier.new(current.lexeme))
if nxt.type != :"\n" && nxt.type != :':'
unexpected_token_error
return
end
fn.params = parse_function_params if nxt.type == :':'
return unless consume_if_nxt_is(build_token(:"\n", "\n"))
fn.body = parse_block
fn
end
#consume_if_nxt_is - আপনি অনুমান করতে পারেন - পরবর্তী টোকেন একটি প্রদত্ত ধরনের হলে আমাদের পয়েন্টার অগ্রসর হবে। অন্যথায়, এটি @errors-এ একটি ত্রুটি যোগ করে . #consume_if_nxt_is খুব দরকারী - এবং অনেক পার্সার পদ্ধতিতে ব্যবহৃত হয় - যখন আমরা টোকেনগুলির গঠন পরীক্ষা করতে চাই যে আমাদের বৈধ বাক্য গঠন আছে কিনা। এটি করার পরে, বর্তমান টোকেনটি :identifier টাইপের (আমরা 'ডাবল' পরিচালনা করছি , ফাংশনের নাম), এবং আমরা একটি AST::Identifier তৈরি করি এবং একটি ফাংশন সংজ্ঞা (AST::FunctionDefinition প্রতিনিধিত্ব করার জন্য একটি নোড তৈরি করার জন্য কনস্ট্রাক্টরের কাছে পাঠান ) আমরা এখানে এটি বিস্তারিতভাবে দেখতে যাচ্ছি না, তবে মূলত, একটি AST::FunctionDefinition নোড ফাংশনের নাম আশা করে, সম্ভাব্য প্যারামিটারের একটি অ্যারে এবং ফাংশন বডি।
#parse_function_definition-এর পরবর্তী ধাপ শনাক্তকারীর পরের টোকেনটি একটি এক্সপ্রেশন টার্মিনেটর (যেমন, প্যারাম ছাড়া একটি ফাংশন) বা একটি কোলন (অর্থাৎ, এক বা একাধিক পরামিতি সহ একটি ফাংশন) কিনা তা যাচাই করা। আমাদের যদি প্যারামিটার থাকে, যেমনটি ডাবল এর ক্ষেত্রে ফাংশন আমরা সংজ্ঞায়িত করছি, আমরা #parse_function_params কল করি তাদের পার্স করতে। আমরা কিছুক্ষণের মধ্যে এই পদ্ধতিটি পরীক্ষা করে দেখব, তবে চলুন প্রথমে চালিয়ে যাই এবং #parse_function_definition এর অন্বেষণ শেষ করি .
ফাংশনের নাম + প্যারামসের পরে একটি টার্মিনেটর আছে কিনা তা যাচাই করার জন্য শেষ ধাপে আরেকটি সিনট্যাক্স পরীক্ষা করা এবং তারপরে, #parse_block কল করে ফাংশন বডি পার্স করতে এগিয়ে যান। . অবশেষে, আমরা fn ফেরত দিই , যা আমাদের সম্পূর্ণরূপে তৈরি AST::FunctionDefinition ধারণ করে উদাহরণ, একটি ফাংশনের নাম, প্যারামিটার এবং একটি বডি দিয়ে সম্পূর্ণ করুন।
ফাংশন প্যারামিটার পার্সিং এর বাদাম এবং বোল্ট
পূর্ববর্তী বিভাগে, আমরা #parse_function_params দেখেছি #parse_function_definition-এর ভিতরে ডাকা হয় . যদি আমরা আমাদের পার্সারের এক্সিকিউশন প্রবাহ এবং অবস্থার সংক্ষিপ্তসারে আমাদের টেবিলে ফিরে যাই, আমরা দেখতে পাব যে কখন #parse_function_params চলতে শুরু করে, বর্তমান টোকেনটি :identifier টাইপের , এবং পরেরটি হল :":" (অর্থাৎ, আমরা সবেমাত্র ফাংশনের নাম পার্সিং শেষ করেছি)। এই সমস্ত কিছু মাথায় রেখে, আসুন আরও কিছু কোড দেখি:
def parse_function_params
consume
return unless consume_if_nxt_is(build_token(:identifier))
identifiers = []
identifiers << AST::Identifier.new(current.lexeme)
while nxt.type == :','
consume
return unless consume_if_nxt_is(build_token(:identifier))
identifiers << AST::Identifier.new(current.lexeme)
end
identifiers
end
এই পদ্ধতির প্রতিটি অংশ ব্যাখ্যা করার আগে, আসুন আমরা যে টোকেনগুলিকে প্রক্রিয়া করতে হবে এবং আমরা এই কাজে কোথায় আছি তা সংক্ষেপে বর্ণনা করি:
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
# here ▲
#parse_function_params-এর প্রথম অংশ সোজা। যদি আমাদের বৈধ সিনট্যাক্স থাকে (: এর পরে অন্তত একটি শনাক্তকারী ), আমরা শেষ পর্যন্ত আমাদের পয়েন্টারকে দুটি অবস্থানে নিয়ে যাই:
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
# ▲
এখন, আমরা পার্স করার প্রথম প্যারামিটারে বসে আছি ( :identifier টাইপের একটি টোকেন ) প্রত্যাশিত হিসাবে, আমরা একটি AST::Identifier তৈরি করি এবং পার্স করা বাকি একাধিক অন্যান্য প্যারামিটারের একটি অ্যারেতে এটিকে পুশ করুন। #parse_function_params-এর পরবর্তী বিটে , যতক্ষণ পর্যন্ত প্যারামিটার বিভাজক (অর্থাৎ, :',' টাইপের টোকেন থাকে ততক্ষণ আমরা প্যারাম পার্সিং চালিয়ে যাই ) আমরা স্থানীয় var identifiers ফেরত দিয়ে পদ্ধতিটি শেষ করি , সম্ভাব্য, একাধিক AST::Identifier সহ একটি অ্যারে নোড, প্রতিটি একটি প্যারাম প্রতিনিধিত্ব করে। যাইহোক, আমাদের ক্ষেত্রে, এই অ্যারের শুধুমাত্র একটি উপাদান আছে।
ফাংশন বডি সম্পর্কে কী?
এখন একটি ফাংশনের সংজ্ঞা পার্স করার শেষ অংশে গভীরভাবে ডুব দেওয়া যাক:এর শরীরের সাথে কাজ করা। যখন #parse_block বলা হয়, আমরা টার্মিনেটরে বসে আছি যা ফাংশন প্যারামিটারের তালিকার শেষে চিহ্নিত করেছে:
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
# ▲
And, here's the implementation of #parse_block :
def parse_block
consume
block = AST::Block.new
while current.type != :end && current.type != :eof && nxt.type != :else
expr = parse_expr_recursively
block << expr unless expr.nil?
consume
end
unexpected_token_error(build_token(:eof)) if current.type == :eof
block
end
AST::Block is the AST node for representing, well, a block of code. In other words, AST::Block just holds a list of expressions, in a very similar fashion as the root node of our program, an AST::Program node (as we saw at the beginning of this post). To parse the block (i.e., the function body), we continue advancing through unprocessed tokens until we encounter a token that marks the end of the block.
To parse the expressions that compose the block, we use our already-known #parse_expr_recursively . We will step into this method call in just a moment; this is the point in which we will start parsing the product operation happening inside our double function. Following this closely will allow us to understand the use of precedence values inside #parse_expr_recursively and how an infix operator (the * in our case) gets dealt with. Before we do that, however, let's finish our exploration of #parse_block .
Before returning an AST node representing our block, we check whether the current token is of type :eof . If this is the case, we have a syntax error since Stoffle requires a block to end with the end keyword. To wrap up the explanation of #parse_block , I should mention something you have probably noticed; one of the conditions of our loop verifies whether the next token is of type :else . This happens because #parse_block is shared by other parsing methods, including the methods responsible for parsing conditionals and loops. Pretty neat, huh?!
Parsing Infix Operators
The name may sound a bit fancy, but infix operators are, basically, those we are very used to seeing in arithmetic, plus some others that we may be more familiar with by being software developers:
module Stoffle
class Parser
# ...
BINARY_OPERATORS = [:'+', :'-', :'*', :'/', :'==', :'!=', :'>', :'<', :'>=', :'<='].freeze
LOGICAL_OPERATORS = [:or, :and].freeze
# ...
end
end
They are expected to be used infixed when the infix notation is used, as is the case with Stoffle, which means they should appear in the middle of their two operands (e.g., as * appears in num * 2 in our double function). Something worth mentioning is that although the infix notation is pretty popular, there are other ways of positioning operators in relation to their operands. If you are curious, research a little bit about "Polish notation" and "reverse Polish notation" methods.
To finish parsing our double function, we have to deal with the * operator:
fn double: num
num * 2
end
In the previous section, we mentioned that parsing the expression that composes the body of double starts when #parse_expr_recursively is called within #parse_block . When that happens, here's our position in @tokens :
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
# ▲
And, to refresh our memory, here's the code for #parse_expr_recursively again:
def parse_expr_recursively(precedence = LOWEST_PRECEDENCE)
parsing_function = determine_parsing_function
if parsing_function.nil?
unrecognized_token_error
return
end
expr = send(parsing_function)
return if expr.nil? # When expr is nil, it means we have reached a \n or a eof.
# Note that here, we are checking the NEXT token.
while nxt_not_terminator? && precedence < nxt_precedence
infix_parsing_function = determine_infix_function(nxt)
return expr if infix_parsing_function.nil?
consume
expr = send(infix_parsing_function, expr)
end
expr
end
In the first part of the method, we will use the same #parse_identifier method we used to parse the num variable. Then, for the first time, the conditions of the while loop will evaluate to true; the next token is not a terminator, and the precedence of the next token is greater than the precedence of this current execution of parse_expr_recursively (precedence is the default, 0, while nxt_precedence returns 6 since the next token is of type :'*' ) This indicates that the node we already built (an AST::Identifier representing num ) will probably be deeper in our AST (i.e., it will be the child of a node yet to be built). We enter the loop and call #determine_infix_function , passing to it the next token (the * ):
def determine_infix_function(token = current)
if (BINARY_OPERATORS + LOGICAL_OPERATORS).include?(token.type)
:parse_binary_operator
elsif token.type == :'('
:parse_function_call
end
end
Since * is a binary operator, running #determine_infix_function will result in :parse_binary_operator . Back in #parse_expr_recursively , we will advance our tokens pointer by one position and then call #parse_binary_operator , passing along the value of expr (the AST::Identifier representing num ):
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
#▲
def parse_binary_operator(left)
op = AST::BinaryOperator.new(current.type, left)
op_precedence = current_precedence
consume
op.right = parse_expr_recursively(op_precedence)
op
end
class Stoffle::AST::BinaryOperator < Stoffle::AST::Expression
attr_accessor :operator, :left, :right
def initialize(operator, left = nil, right = nil)
@operator = operator
@left = left
@right = right
end
def ==(other)
operator == other&.operator && children == other&.children
end
def children
[left, right]
end
end
At #parse_binary_operator , we create an AST::BinaryOperator (its implementation is shown above if you are curious) to represent * , setting its left operand to the identifier (num ) we received from #parse_expr_recursively . Then, we save the precedence value of * at the local var op_precedence and advance our token pointer. To finish building our node representing * , we call #parse_expr_recursively again! We need to proceed in this fashion because the right-hand side of our operator will not always be a single number or identifier; it can be a more complex expression, such as something like num * (2 + 2) .
One thing of utmost importance that happens here at #parse_binary_operator is the way in which we call #parse_expr_recursively back again. We call it passing 6 as a precedence value (the precedence of * , stored at op_precedence ) Here we observe an important aspect of our parsing algorithm, which was mentioned previously. By passing a relatively high precedence value, it seems like * is pulling the next token as its operand. Imagine we were parsing an expression like num * 2 + 1; in this case, the precedence value of * passed in to this next call to #parse_expr_recursively would guarantee that the 2 would end up being the right-hand side of * and not an operand of + , which has a lower precedence value of 5 .
After #parse_expr_recursively returns an AST::Number node, we set it as the right-hand size of * and, finally, return our complete AST::BinaryOperator node. At this point, we have, basically, finished parsing our Stoffle program. We still have to parse some terminator tokens, but this is straightforward and not very interesting. At the end, we will have an AST::Program instance at @ast with expressions that could be visually represented as the tree we saw at the beginning of this post and in the introduction to the second section of the post:

Wrapping Up
In this post, we covered the principal aspects of Stoffle's parser. If you understand the bits we explored here, you shouldn't have much trouble understanding other parser methods we were not able to cover, such as parsing conditionals and loops. I encourage you to explore the source code of the parser by yourself and tweak the implementation if you are feeling more adventurous! The implementation is accompanied by a comprehensive test suite, so don't be afraid to try things out and mess up with the parser.
In subsequent posts in this series, we will finally breathe life into our little monster by implementing the last bit we are missing:the tree-walk interpreter. I can't wait to be there with you as we run our first Stoffle program!


