রুবির সাথে মার্জ সাজানোর অন্বেষণ

এটি রুবির সাথে বিভিন্ন সাজানোর অ্যালগরিদম বাস্তবায়নের দিকে লক্ষ্য করা একটি সিরিজের অংশ 3। পার্ট 1 অন্বেষণ করা বুদবুদ বাছাই, এবং অংশ 2 অন্বেষণ করা নির্বাচন বাছাই৷
৷

যেমনটি আমরা এই সিরিজের আগের পোস্টগুলিতে আলোচনা করেছি, ডেটা কীভাবে সাজাতে হয় তা বোঝা যে কোনও সফ্টওয়্যার ইঞ্জিনিয়ারের টুলকিটের একটি অবিচ্ছেদ্য অংশ। সৌভাগ্যবশত, রুবির মতো বেশিরভাগ উচ্চ-স্তরের ভাষাগুলিতে ইতিমধ্যেই অন্তর্নির্মিত পদ্ধতি রয়েছে যা অ্যারে সাজানোর ক্ষেত্রে দক্ষ। উদাহরণস্বরূপ, যখন আপনি .sort কল করেন একটি অ্যারেতে, আপনি হুডের নিচে কুইকসর্ট ব্যবহার করছেন। এই পোস্টে, আমরা দ্রুত সাজানোর জন্য একটি অনুরূপ অ্যালগরিদম শিখতে যাচ্ছি -- মার্জ সর্ট। এই উভয় অ্যালগরিদম একটি "বিভাজন এবং জয় করার পদ্ধতি" ব্যবহার করে। মার্জ সর্ট 1945 সালে জন ভন নিউম্যান আবিষ্কার করেছিলেন। ভন নিউম্যান ছিলেন একজন বিখ্যাত কম্পিউটার বিজ্ঞানী এবং পদার্থবিদ যিনি ম্যানহাটন প্রকল্প, "মিনি-ম্যাক্স" উপপাদ্য, মন্টে কার্লো পদ্ধতি এবং আরও অনেক কিছুতে কাজ করার জন্যও পরিচিত।

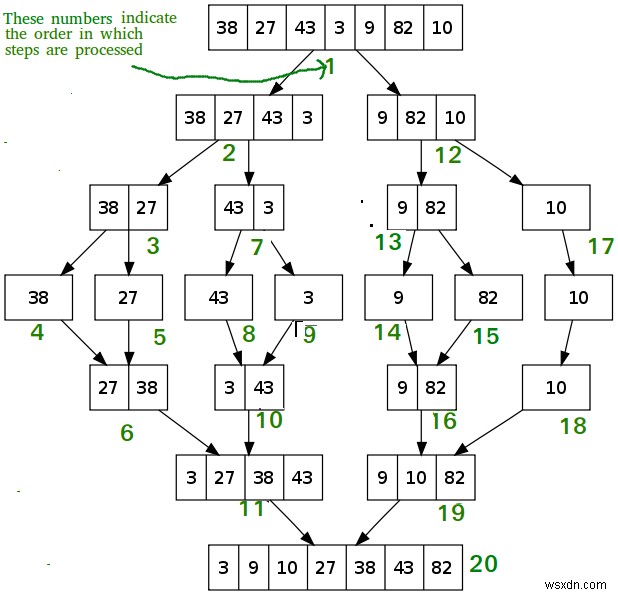
একটি উচ্চ স্তরে, মার্জ সর্ট অ্যালগরিদম অ্যারেটিকে দুটি সাব-অ্যারেতে বিভক্ত করে বারবার (পুনরাবৃত্তি ব্যবহার করে) যতক্ষণ না শুধুমাত্র একটি উপাদান অবশিষ্ট থাকে। সেখান থেকে, উপাদানগুলি আবার "একত্রিত" হয়ে চূড়ান্ত, সাজানো অ্যারে তৈরি করে। বুদ্বুদ সাজানো এবং অন্যান্য অনুরূপ অ্যালগরিদমগুলির বিপরীতে, মার্জ সাজানো ভিজ্যুয়ালাইজেশন ছাড়া বোঝা কঠিন। নিম্নোক্ত চিত্রটি উইকিপিডিয়ার একটি ধাপে ধাপে চিত্র দেখানো হয়েছে কিভাবে মার্জ সর্ট কাজ করে। যাইহোক, চিন্তা করবেন না যদি আপনি এখনও কি ঘটছে তা নিয়ে কিছুটা অস্পষ্ট হন; আমরা পরবর্তী কোডের মাধ্যমে কাজ করব।

আমরা পূর্বে আলোচনা করেছি এমন অ্যালগরিদমগুলির বিপরীতে (অর্থাৎ, বুদ্বুদ এবং নির্বাচন), যা মূলত যে কোনও বাস্তব কাজের জন্য অব্যবহারিক ছিল, বিগ-ও স্বরলিপির ক্ষেত্রে মার্জ সর্ট অনেক ভাল কাজ করে৷ আপনি যদি Big-O স্বরলিপির সাথে অপরিচিত হন তবে এটি বিভিন্ন অ্যালগরিদমের সবচেয়ে খারাপ-কেস কর্মক্ষমতা উপস্থাপন করে। এটি আমাদের সহজেই তাদের বিগ-ও-এর উপর ভিত্তি করে অ্যালগরিদম তুলনা করতে দেয়। উদাহরণ স্বরূপ, O(1) এর একটি বিগ-ও সহ একটি অ্যালগরিদমের অর্থ হল সবচেয়ে খারাপ-কেস রান-টাইমটি ধ্রুবক থাকে কারণ উপাদানগুলির সংখ্যা, "n" বৃদ্ধি পায়, যেখানে O(এর বিগ-ও স্বরলিপি সহ একটি অ্যালগরিদম n) মানে সবচেয়ে খারাপ-কেস রান-টাইম n বাড়ার সাথে সাথে রৈখিকভাবে বৃদ্ধি পায়। এর মানে হল যে আপনার যদি 100টি উপাদান সহ একটি অ্যারে থাকে এবং অবশ্যই O(n) এবং O(1) বাছাই করা অ্যালগরিদমগুলির মধ্যে বেছে নিতে হবে, আপনি O(1) অ্যালগরিদম বেছে নেবেন কারণ O(1) অবশ্যই O(100) কে হারায়। বুদবুদ এবং নির্বাচন সাজানোর অ্যালগরিদম উভয়েরই O(n^2) এর সবচেয়ে খারাপ কেস রয়েছে। এটি খুব দরকারী নয় কারণ এর অর্থ হল অ্যালগরিদম উপাদানের সংখ্যা বৃদ্ধির সাথে সাথে অত্যন্ত ধীরে ধীরে কাজ করবে। বিপরীতে, মার্জ সর্ট n log(n) এ সঞ্চালিত হয়, যার অর্থ অ্যালগরিদম বুদ্বুদ বা নির্বাচন সাজানোর মতো দক্ষতার ত্যাগ করবে না।

চলুন ডায়াগ্রামে উদাহরণ দিয়ে হাঁটা যাক। আমরা [38, 27, 43, 3, 9, 82, 10] এর অ্যারে দিয়ে শুরু করি এবং তারপরে অ্যারেটিকে অর্ধেক ভাগ করুন যতক্ষণ না আমরা একক উপাদান রেখে যাচ্ছি।

আমরা প্রারম্ভিক অ্যারেটিকে দুটি ভাগে ভাগ করেছি:[38, 27, 43, 3] এবং [9, 82, 10] .
আমরা আবার প্রথম অর্ধেক ভাগ করেছি:[38, 27] এবং [43, 3] .
আমরা প্রথমার্ধকে একক উপাদানে বিভক্ত করি:[38] , [27] , [43] , এবং [3] .
আমরা [27, 38] তৈরি করতে 38 এবং 27 সাজাই এবং 48 এবং 3 [3, 43] তৈরি করতে .
এগুলিকে একসাথে রাখলে, আমাদের আছে [3, 27, 38, 43] .
এখন, আমরা মূল অ্যারের দ্বিতীয়ার্ধে চলে যাই, যেটি ছিল [9, 82, 10] . আমরা এটিকে অর্ধেক ভাগ করে [9, 82] পাই এবং [10] .
আমরা [9, 82] বিভক্ত করেছি [9]-এ এবং [82] , এবং তারপর আমাদের আছে [10] , যা ইতিমধ্যেই একবচন৷
আমরা [9, 82] সাজাই একসাথে ফিরে যান এবং তারপর [10] মার্জ করুন ফিরে আসে, ফলে [9, 10, 82] .
অবশেষে, আমরা [3, 27, 38, 43] মার্জ করি এবং [9, 10, 82] পেতে [3, 9, 10, 27, 38, 43, 82] .

একটি রুবি বাস্তবায়ন

নিম্নলিখিতটি রুবিতে লেখা একটি মার্জ সর্ট অ্যালগরিদম:

class MergeSort
  def sort(numbers)

    num_elements = numbers.length
    if num_elements <= 1
      return numbers
    end

    half_of_elements = (num_elements / 2).round

    left  = numbers.take(half_of_elements)
    right = numbers.drop(half_of_elements)

    sorted_left = sort(left)
    sorted_right = sort(right)

    merge(sorted_left, sorted_right)
  end

  def merge(left_array, right_array)
    if right_array.empty?
      return left_array
    end

    if left_array.empty?
      return right_array
    end

    smallest_number = if left_array.first <= right_array.first
      left_array.shift
    else
      right_array.shift
    end

    recursive = merge(left_array, right_array)

    [smallest_number].concat(recursive)
  end
end

আসুন এখানে কি ঘটছে মাধ্যমে হাঁটা. প্রথমে, আমরা sort-এ ফোকাস করব উপরের পদ্ধতি।

  def sort(numbers)

    num_elements = numbers.length
    if num_elements <= 1
      return numbers
    end

    half_of_elements = (num_elements / 2).round

    left  = numbers.take(half_of_elements)
    right = numbers.drop(half_of_elements)

    sorted_left = sort(left)
    sorted_right = sort(right)

    merge(sorted_left, sorted_right)
  end

কোডের এই অংশের লক্ষ্য হল প্রদত্ত সংখ্যাগুলিকে অর্ধেক ভাগ করা যতক্ষণ না আমাদের প্রতিটিতে একটি মাত্র আইটেম বাকি থাকে। এটিকে কার্যকরভাবে দেখতে, শেষ লাইনটি মন্তব্য করুন (একত্রিত করুন(sorted_left, sorted_right)) এবং পরিবর্তে, sorted_left প্রিন্ট আউট করুন এবং sorted_right . আমাদের উদাহরণ অ্যারেতে পাস করে প্রোগ্রামটি চালানো, আপনার টার্মিনালে এটি দেখতে হবে:

merge_sort = MergeSort.new
puts merge_sort.sort([38, 27, 43, 3, 9, 82, 10])

ruby ruby-merge-sort.rb

দারুণ! আমাদের কোড আমাদের প্রাথমিক অ্যারে নিয়েছে এবং এটিকে অর্ধেক ভাগ করেছে। চলুন merge দেখে নেওয়া যাক কোডের পরবর্তী অংশ।

  def merge(left_array, right_array)
    if right_array.empty?
      return left_array
    end

    if left_array.empty?
      return right_array
    end

    smallest_number = if left_array.first <= right_array.first
      left_array.shift
    else
      right_array.shift
    end

    recursive = merge(left_array, right_array)

    [smallest_number].concat(recursive)
  end

প্রথমে, আমরা সাব-অ্যারেগুলির মধ্যে একটি খালি কিনা তা পরীক্ষা করি। যদি তাই হয়, আমরা কেবল অন্যটি ফেরত দিতে পারি। অন্যথায়, উভয় সাব-অ্যারে খালি না থাকায়, আমরা প্রতিটি অ্যারের প্রথম উপাদানের মান তুলনা করি এবং তারপরে একটি অসীম লুপ তৈরি রোধ করতে তুলনামূলক মানগুলি স্থানান্তর করি। এরপরে, আমরা মূল অ্যারেতে রিকারশন ব্যবহার করি (এক সেকেন্ডে আরও!) যতক্ষণ না আমরা শেষ পর্যন্ত দুটি অ্যারেকে একসাথে সংযুক্ত করতে পারি, সুন্দরভাবে সাজানো।

পুনরাবৃত্তিতে আরও কিছুটা

যদি এমন কিছু থাকে যা আমাদের কোডে অদ্ভুত দেখায়, আমার অনুমান এটি এই লাইন:recursive = merge(left_array, right_array) আমরা আমাদের merge কে কল করছি নিজের মধ্যেই থেকে পদ্ধতি . ছিঃ! একে আমরা বলি রিকারশন -- এমন একটি কৌশল যেখানে একটি নির্দিষ্ট শর্ত পূরণ না হওয়া পর্যন্ত একটি ফাংশন এক বা একাধিকবার নিজেকে কল করে। আমাদের ক্ষেত্রে, merge বাম বা ডান অ্যারে খালি না হওয়া পর্যন্ত কল করা চলবে। আপনি যদি পুনরাবৃত্ত সম্পর্কে আরও জানতে আগ্রহী হন, তাহলে এখানে একটি উদাহরণ রয়েছে যা ফিবোনাচি সিকোয়েন্সের জন্য একটি ফাংশন লিখতে রুবি এবং পুনরাবৃত্তি ব্যবহার করে চলে।

র্যাপ-আপ

৷

আমি আশা করি আপনি মার্জ সাজানোর বিষয়ে আরও শিখতে উপভোগ করেছেন! এটি কীভাবে উচ্চ স্তরে কাজ করে, সেইসাথে কেন এটি বুদবুদ বা নির্বাচনের সাজানোর চেয়ে আরও দক্ষ পছন্দ তা বোঝা সম্ভবত চাকরির ইন্টারভিউ বা আপনার প্রতিদিনের কাজগুলিতে কার্যকর হবে। এছাড়াও, একাধিক মার্জ সাজানোর ভেরিয়েন্ট রয়েছে যা আপনি আগ্রহী হলে উইকিপিডিয়াতে এটি সম্পর্কে আরও পড়তে পারেন। পরের বার পর্যন্ত... খুশি বাছাই!