BST এর উপাদানগুলিকে উপস্থাপন করার জন্য আমাদের কাছে দুটি অ্যারে রয়েছে। যদি আমরা সেই অ্যারে থেকে বাম থেকে ডানে উপাদান নিই এবং BST গঠন করি, তাহলে উভয় অ্যারে থেকে নিয়ে আমরা একই BST তৈরি করব। আমাদের পরীক্ষা করতে হবে যে উভয়ই একই গঠন করছে কি না। কিন্তু প্রতিবন্ধকতা হল আমরা BST বানাতে পারি না। ধরুন দুটি অ্যারে হল {2, 4, 1, 3} এবং {2, 1, 4, 3}, তাহলে আমরা যদি দেখি, এই দুটি ক্রম একই BST গঠন করতে পারে।
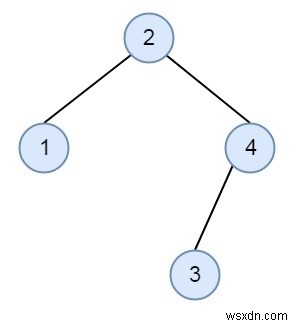
পদ্ধতি সহজ. আমরা জানি, বাম উপবৃক্ষের উপাদানগুলি মূলের চেয়ে ছোট এবং ডান উপবৃক্ষের উপাদানগুলি মূলের চেয়ে বড়। এই দুটি তালিকা একই BST প্রতিনিধিত্ব করতে পারে যদি প্রতিটি উপাদান x এর জন্য, x এর বাম এবং ডান উপবৃক্ষের উপাদানগুলি উভয় অ্যারেতে এর পরে উপস্থিত হয়। বাম এবং ডান উপবৃক্ষের শিকড়ের ক্ষেত্রেও একই কথা। আমরা পরীক্ষা করব যে পরবর্তী ছোট এবং বড় উপাদান উভয় অ্যারেতে একই কিনা। এই একই সম্পত্তি বাম এবং ডান সাবট্রির জন্য বারবার চেক করা হয়।
উদাহরণ
#include <iostream>
using namespace std;
bool isSameCheckHelper(int tree1[], int tree2[], int n, int i1, int i2, int min, int max) {
int j, k;
for (j = i1; j < n; j++)
if (tree1[j] > min && tree1[j] < max)
break;
for (k = i2; k < n; k++)
if (tree2[k] > min && tree2[k] < max)
break;
if (j==n && k==n) //If the parent element is leaf in both arrays
return true;
if (((j==n)^(k==n)) || tree1[j]!=tree2[k])
return false;
return isSameCheckHelper(tree1, tree2, n, j+1, k+1, tree1[j], max) &&
// for Right Subtree
isSameCheckHelper(tree1, tree2, n, j+1, k+1, min, tree1[j]); // for Left Subtree
}
bool areBSTSame(int first[], int second[], int n) {
return isSameCheckHelper(first, second, n, 0, 0, INT_MIN, INT_MAX);
}
int main() {
int first[] = {8, 3, 6, 1, 4, 7, 10, 14, 13};
int second[] = {8, 10, 14, 3, 6, 4, 1, 7, 13};
int n=sizeof(first)/sizeof(first[0]);
if(areBSTSame(first, second, n)) {
cout << "Two BSTs are same";
} else {
cout << "Two BSTs are not same";
}
} আউটপুট
Two BSTs are same


