বিভিন্ন অক্ষরের একটি ম্যাট্রিক্স দেওয়া আছে। একটি অক্ষর থেকে শুরু করে বর্তমান অক্ষরের চেয়ে বড় সমস্ত অক্ষর অতিক্রম করে আমাদের দীর্ঘতম পথ খুঁজে বের করতে হবে। অক্ষরগুলো একে অপরের সাথে পরপর।
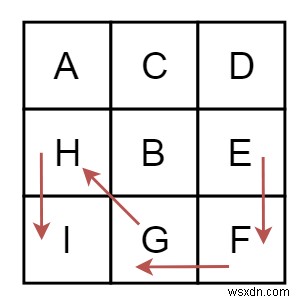
E.
থেকে শুরু হয়দীর্ঘতম পথ খুঁজে পেতে, আমরা গভীরতার প্রথম অনুসন্ধান অ্যালগরিদম ব্যবহার করব। DFS চলাকালীন, কিছু উপ-সমস্যা একাধিকবার দেখা দিতে পারে। বারবার সেই সাব সমস্যার গণনা এড়াতে, আমরা ডায়নামিক প্রোগ্রামিং পদ্ধতি ব্যবহার করব।
উদাহরণ
#include<iostream>
#define ROW 3
#define COL 3
using namespace std;
// tool matrices to recur for adjacent cells.
int x[] = {0, 1, 1, -1, 1, 0, -1, -1};
int y[] = {1, 0, 1, 1, -1, -1, 0, -1};
int longestPath[ROW][COL];
char mat[ROW][COL] = {
{'a','c','d'},
{'h','b','a'},
{'i','g','f'}
};
int max(int a, int b){
return (a>b)?a:b;
}
bool isvalid(int i, int j){
if (i < 0 || j < 0 || i >= ROW || j >= COL) //when i and j are in range
return false;
return true;
}
bool isadjacent(char previous, char current){
return ((current - previous) == 1); //check current and previous are adjacent or not
}
int findLongestLen(int i, int j, char prev){
if (!isvalid(i, j) || !isadjacent(prev, mat[i][j]))
//when already included or not adjacent
return 0;
if (longestPath[i][j] != -1)
return longestPath[i][j]; //subproblems are solved already
int len = 0; // Initialize result to 0
for (int k=0; k<8; k++) //find length of the largest path recursively
len = max(len, 1 + findLongestLen(i + x[k], j + y[k], mat[i][j]));
return longestPath[i][j] = len; // save the length and return
}
int getLen(char start){
for(int i = 0; i<ROW; i++)
for(int j = 0; j<COL; j++)
longestPath[i][j] = -1; //set all elements to -1
int len = 0;
for (int i=0; i<ROW; i++){
for (int j=0; j<COL; j++){ // check for all possible starting point
if (mat[i][j] == start) {
for (int k=0; k<8; k++) //for all eight adjacent cells
len = max(len, 1 + findLongestLen(i + x[k], j + y[k], start));
}
}
}
return len;
}
int main() {
char start;
cout << "Enter Starting Point (a-i): "; cin >> start;
cout << "Maximum consecutive path: " << getLen(start);
return 0;
} আউটপুট
Enter Starting Point (a-i): e Maximum consecutive path: 5


