ধারণা
একটি প্রদত্ত গ্রাফের ক্ষেত্রে, গ্রাফের একটি উত্স শীর্ষবিন্দু এবং একটি সংখ্যা k (এখানে k দ্বারা উৎস শীর্ষ এবং গন্তব্য শীর্ষবিন্দুর মধ্যে গ্রাফের পথের দৈর্ঘ্য নির্দেশ করা হয়েছে), আমাদের কাজ হল একটি সহজ পথ (কোনও চক্র ছাড়া) শুরু হয়েছে কিনা তা নির্ধারণ করা। প্রদত্ত উত্স থেকে এবং অন্য কোন শীর্ষে শেষ হয় (অর্থাৎ গন্তব্য)। গ্রাফটি নিম্নলিখিত −
এ দেখানো হয়েছে
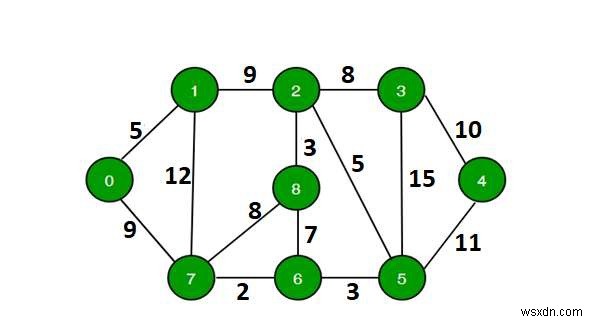
ইনপুট
Source s = 0, k = 64
আউটপুট
True
একটি সহজ পথ রয়েছে 0 -> 7 -> 1-> 2 -> 8 -> 6 -> 5 -> 3 -> 4, যার মোট দূরত্ব 68 কিমি যা 64-এর বেশি৷
ইনপুট
Source s = 0, k = 70
আউটপুট
False
উপরের গ্রাফে, দীর্ঘতম সরল পাথের দূরত্ব 69 (0 -> 7 -> 1-> 2 -> 3 -> 4 -> 5-> 6 -> 8, 69-এর বেশি ইনপুটের জন্য সউটপুট মিথ্যা হওয়া উচিত।
পদ্ধতি
এটা উল্লেখ করা উচিত যে একটি গুরুত্বপূর্ণ বিষয় হল BFS(Breadth First Search) অথবা DFS(ডেপথ ফার্স্ট সার্চ) করা এবং প্রতিটি ধাপে দীর্ঘতম প্রান্তটি নির্বাচন করা কাজ করবে না। এর পিছনে কারণ হল একটি ছোট প্রান্ত দীর্ঘ পথ তৈরি করতে পারে কারণ এটির মাধ্যমে সংযুক্ত উচ্চতর ওয়েটেজ।
এখন ধারণাটি ব্যাকট্র্যাকিং বাস্তবায়ন করা। এই ক্ষেত্রে, আমরা প্রদত্ত উত্স থেকে শুরু করি; বর্তমান শীর্ষবিন্দু থেকে সমস্তপথ অতিক্রম করুন। এখানে, আমরা উৎস থেকে বর্তমান দূরত্বের ট্র্যাক বজায় রাখি। দেখা গেছে দূরত্ব k-এর চেয়ে বেশি হলে আমরা সত্যে ফিরে আসি। কিন্তু বিকল্পের ক্ষেত্রে যাতে কোনো পথ যদি k-এর বেশি দূরত্ব তৈরি না করে, আমরা পিছিয়ে যাই।
এখন প্রশ্ন উঠছে যে আমরা কীভাবে নিশ্চিত করব যে পথটি সহজ এবং আমরা অ্যাসাইকেলে লুপ করব না? এখানে ধারণাটি একটি অ্যারেতে বর্তমান পথের শীর্ষবিন্দুগুলির ট্র্যাক বজায় রাখা। এই ক্ষেত্রে, যখনই আমরা পাথে একটি শীর্ষবিন্দু যোগ করি, আমরা যাচাই করি যে এটি ইতিমধ্যে বিদ্যমান কিনা বর্তমান পাথে নেই। এটা দেখা গেছে যে এটি বিদ্যমান থাকলে, আমরা প্রান্তকে উপেক্ষা করি।
উদাহরণ
// Program to find if there is a simple path with
// weight more than k
#include<bits/stdc++.h>
using namespace std;
// iPair ==> Integer Pair
typedef pair<int, int> iPair;
// Now this class represents a dipathted graph using
// adjacency list representation
class Graph{
int V1; // Indicates no. of vertices
// In this case, in a weighted graph, we need to store vertex
// and weight pair for every edge
list< pair<int, int>> *adj1;
bool pathMoreThanKUtil(int src1, int k, vector<bool>&path1);
public:
Graph(int V1); // Shows constructor
// Shows function to add an edge to graph
void addEdge(int u1, int v1, int w1);
bool pathMoreThanK(int src1, int k);
};
// Used to return true if graph has path more than k length
bool Graph::pathMoreThanK(int src1, int k){
// Used to create a path array with nothing included
// in path
vector<bool> path1(V1, false);
// Used to add source vertex to path
path1[src1] = 1;
return pathMoreThanKUtil(src1, k, path1);
}
// Used to print shortest paths from src to all other vertices
bool Graph::pathMoreThanKUtil(int src1, int k, vector<bool>&path1){
// Now if k is 0 or negative, return true;
if (k <= 0)
return true;
//Used to get all adjacent vertices of source vertex src and
// recursively explore all paths from src.
list<iPair>::iterator i;
for (i = adj1[src1].begin(); i != adj1[src1].end(); ++i){
// Used to get adjacent vertex and weight of edge
int v1 = (*i).first;
int w1 = (*i).second;
// Now if vertex v is already there in path, then
// there is a cycle (we ignore this edge)
if (path1[v1] == true)
continue;
// Now if weight of is more than k, return true
if (w1 >= k)
return true;
// Else add this vertex to path
path1[v1] = true;
// Now if this adjacent can provide a path longer
// than k, return true.
if (pathMoreThanKUtil(v1, k-w1, path1))
return true;
// Backtrack
path1[v1] = false;
}
// Now if no adjacent could produce longer path, return
// false
return false;
}
// Used to allocates memory for adjacency list
Graph::Graph(int V1){
this->V1 = V1;
adj1 = new list<iPair> [V1];
}
//Shows utility function to an edge (u, v) of weight w
void Graph::addEdge(int u1, int v1, int w1){
adj1[u1].push_back(make_pair(v1, w1));
adj1[v1].push_back(make_pair(u1, w1));
}
// Driver program to test methods of graph class
int main(){
// Used to create the graph given in above fugure
int V1 = 9;
Graph g(V1);
// making above shown graph
g.addEdge(0, 1, 5);
g.addEdge(0, 7, 9);
g.addEdge(1, 2, 9);
g.addEdge(1, 7, 12);
g.addEdge(2, 3, 8);
g.addEdge(2, 8, 3);
g.addEdge(2, 5, 10);
g.addEdge(3, 4, 10);
g.addEdge(3, 5, 15);
g.addEdge(4, 5, 11);
g.addEdge(5, 6, 3);
g.addEdge(6, 7, 2);
g.addEdge(6, 8, 7);
g.addEdge(7, 8, 8);
int src1 = 0;
int k = 70;
g.pathMoreThanK(src1, k)? cout << "Yes\n" :
cout << "No\n";
k = 68;
g.pathMoreThanK(src1, k)? cout << "Yes\n" :
cout << "No\n";
return 0;
} আউটপুট
No Yes


