আমাদেরকে স্বতন্ত্র নোডের একটি বাইনারি ট্রি এবং বাইনারি গাছের দুটি নোড দেওয়া হয়েছে যার পাথ বাইনারি ট্রিতে আমরা প্রিন্ট করতে চাই৷
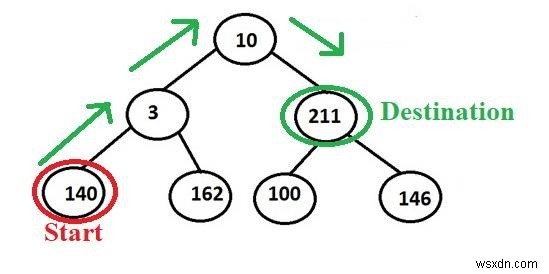
উদাহরণস্বরূপ − আমরা নোড 140 থেকে 211 এর মধ্যে পাথ প্রিন্ট করতে চাই তাই এর আউটপুট −
এর মত হওয়া উচিত।Output: 140->3->10->211
ধারণাটি হল দুটি নোডের রুট নোড গঠনের পাথগুলি খুঁজে বের করা এবং সেগুলিকে দুটি পৃথক ভেক্টর বা অ্যারে বলে path1 এবং path2 বলে৷
এখন, দুটি ভিন্ন কেস দেখা দেয় -
- যদি দুটি নোড রুট নোডের বিভিন্ন সাবট্রিতে থাকে − যখন দুটি নোড বিভিন্ন সাবট্রিতে থাকে যেমন একটি বামে এবং অন্যটি ডানদিকে। এই ক্ষেত্রে, এটা স্পষ্ট যে রুট নোডটি নোড 1 থেকে নোড 2 পর্যন্ত পথের মধ্যে থাকবে। সুতরাং, বিপরীত ক্রমে path1 এবং তারপর path2 প্রিন্ট করুন।
-
যদি নোডগুলি একই সাবট্রিতে থাকে − যখন উভয় নোড একই সাবট্রিতে থাকে যা হয় বাম সাবট্রিতে বা ডান সাবট্রিতে হতে পারে। এই ক্ষেত্রে, আপনাকে রুট থেকে দুটি নোডের পথটি পর্যবেক্ষণ করতে হবে একটি ছেদ বিন্দু থাকবে যার আগে রুট নোড থেকে দুটি নোডের জন্য পথটি সাধারণ। আমাদের ছেদ বিন্দু খুঁজে বের করতে হবে এবং উপরের ক্ষেত্রের মতো সেই বিন্দু থেকে নোডগুলি প্রিন্ট করতে হবে।
অ্যালগরিদম
START STEP 1-> DEFINE A struct Node WITH int data AND Node *left, *right; STEP 2-> DEFINE A TREE STRUCTURE struct Node* tree(int data)FUNCTION bool path(Node* root, vector& arr, int x) STEP 1-> IF root IS NULL RETURN false END IF STEP 2-> arr.push_back(root->data) IF root->data == x THEN RETURN true END IF STEP 3-> IF path(root->left, arr, x) || path(root->right, arr, x) THEN, RETURN true STEP 4-> arr.pop_back() return false END FUNCTION FUNCTION void printPath(Node* root, int n1, int n2) STEP 1-> DEFINE A vector<int> path1 STEP 2-> DEFINE A vector<int> path2 STEP 3-> CALL FUNCTION path(root, path1, n1) STEP 4-> CALL FUNCTION path(root, path2, n2) STEP 5-> DEFINE AND SET intersection = -1, i = 0, j = 0 STEP 6-> LOOP WHILE i != path1.size() || j != path2.size() IF i == j && path1[i] == path2[j] INCREMENT i BY 1 INCREMENT j BY 1 ELSE SET intersection = j - 1 BREAK; END IF END WHILE STEP 7-> LOOP FOR i = path1.size() – 1 AND i > intersection AND i--PRINT path1[i] END FOR STEP 8-> LOOP FOR i = intersection AND i < path2.size() AND i++ PRINT path2[i] END FOR
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
// structure of a node of binary tree
struct Node {
int data;
Node *left, *right;
};
struct Node* tree(int data){
struct Node* newNode = new Node;
newNode->data = data;
newNode->left = newNode->right = NULL;
return newNode;
}
bool path(Node* root, vector<int>& arr, int x){
if (!root)
return false;
// push the node's value in 'arr'
arr.push_back(root->data);
// if it is the required node
// return true
if (root->data == x)
return true;
if (path(root->left, arr, x) || path(root->right, arr, x))
return true;
arr.pop_back();
return false;
}
// Function to print the path between
// any two nodes in a binary tree
void printPath(Node* root, int n1, int n2){
// vector to store the path
vector<int> path1;
vector<int> path2;
path(root, path1, n1);
path(root, path2, n2);
int intersection = -1;
int i = 0, j = 0;
while (i != path1.size() || j != path2.size()) {
if (i == j && path1[i] == path2[j]) {
i++;
j++;
} else {
intersection = j - 1;
break;
}
}
// Print the required path
for (int i = path1.size() - 1; i > intersection; i--)
cout << path1[i] << " ";
for (int i = intersection; i < path2.size(); i++)
cout << path2[i] << " ";
}
int main(){
// binary tree formation
struct Node* root = tree(1);
root->left = tree(2);
root->left->left = tree(4);
root->left->left->left = tree(6);
root->left->right = tree(5);
root->left->right->left = tree(7);
root->left->right->right = tree(8);
root->right = tree(3);
root->right->left = tree(9);
root->right->right = tree(10);
int node1 = 5;
int node2 = 9;
printPath(root, node1, node2);
return 0;
} আউটপুট
এই প্রোগ্রামটি আউটপুট −
প্রিন্ট করবে5 2 1 3 9


