এই সমস্যায়, আমাদের একটি বাইনারি ট্রি দেওয়া হয়েছে প্রতিটি নোডের সাথে একটি মান রয়েছে। আমাদের কাজ হল একটি বাইনারি গাছের দুটি পাতার মধ্যে সর্বাধিক পথের যোগফল খুঁজে বের করার জন্য একটি প্রোগ্রাম তৈরি করা৷
এখানে, আমাদের একটি লিফ নোড থেকে অন্য লিফ নোডের পথ খুঁজে বের করতে হবে যা মানগুলির সর্বাধিক যোগফল প্রদান করবে। এই সর্বোচ্চ যোগফল রুট নোডকে অন্তর্ভুক্ত করতে পারে না।
বাইনারি ট্রি একটি ট্রি ডেটা স্ট্রাকচার যেখানে প্রতিটি নোডে সর্বোচ্চ দুটি চাইল্ড নোড থাকতে পারে। এদেরকে বাম শিশু এবং ডান শিশু বলা হয়।
উদাহরণ −
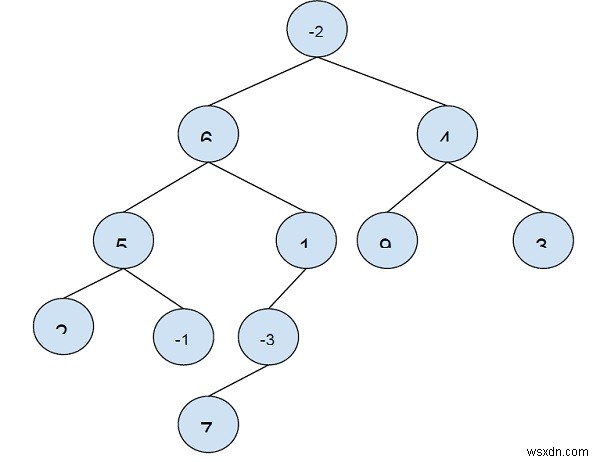
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক -
ইনপুট৷ − //বাইনারি গাছ…
আউটপুট − 24
ব্যাখ্যা − লিফ নোড − 2 থেকে 9 পর্যন্ত পথটি সর্বাধিক যোগফল দেবে যা (2 + 5 + 6 -2 + 4 + 9 ) =24
এই সমস্যার সমাধান করার জন্য, আমরা ট্রি ট্রাভার্সাল করব এবং বর্তমান নোডের জন্য বাম সাব-ট্রি/ডান সাবট্রির জন্য সর্বাধিক যোগফল সংরক্ষণ করব। এছাড়াও, আমরা এখন পর্যন্ত দুটি লিফ নোডের মধ্যে সর্বাধিক পথ খুঁজে পাব।
এর জন্য, প্রতিটি নোড আমরা তার সাবট্রির জন্য সর্বাধিক সম্ভাব্য পাতা থেকে পাতার পথ খুঁজে পাব। এবং তারপর এটিকে সামগ্রিক সর্বাধিক পাথের সাথে তুলনা করুন এবং গ্লোবাল সর্বাধিক পাথ সমষ্টি মানতে উভয় মানের সর্বাধিক সংরক্ষণ করুন৷
আসুন সমাধানটি আরও ভালভাবে বুঝতে আমাদের উদাহরণ থেকে এই সমাধানটি দেখি -
বিশ্বব্যাপী সর্বোচ্চ যোগফল =6 (পাথ 2→5→-1 এর জন্য)
এখন আমরা রুট নোড হিসাবে 6 নিতে পরীক্ষা করব।
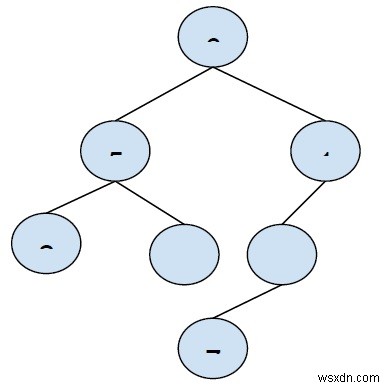
বাম সাবট্রিতে -
লিফ নোড পর্যন্ত পথের যোগফল হল 7 এবং 4।
সর্বাধিক 7 (পাথ 5→2 এর জন্য)।
ডান সাবট্রিতে -
লিফ নোড পর্যন্ত পথের যোগফল পাথের জন্য 5 (1rarr;-3rarr;7) যা একটি সম্ভাব্য পথ।
না, লিফ নোডের মধ্যে পথের যোগফল হল −
বাম সাবট্রিতে পাতা থেকে রুট (6) এর সর্বোচ্চ যোগফল + রুট + ডান সাবট্রিতে পাতা থেকে রুট (6) এর সর্বোচ্চ যোগফল =7 + 6 + 5 =18।
বৈশ্বিক সর্বাধিক পাথ যোগফল(6) এর সাথে তুলনা করে, নতুন বিশ্বব্যাপী সর্বাধিক পাথ যোগফল =18।
উদাহরণ
দুটি লিফ নোডের মধ্যে সর্বাধিক পথের যোগফল খুঁজে বের করার প্রোগ্রাম -
#include <bits/stdc++.h>
using namespace std;
struct Node{
int data;
struct Node* left, *right;
};
struct Node* insertNode(int data){
struct Node* node = new(struct Node);
node->data = data;
node->left = node->right = NULL;
return (node);
}
int max(int a, int b)
{ return (a >= b)? a: b; }
int maxPathSumLeaf(struct Node *root, int &maxSum){
if (root==NULL) return 0;
if (!root->left && !root->right) return root->data;
int leftSubTree = maxPathSumLeaf(root->left, maxSum);
int rightSubTree = maxPathSumLeaf(root->right, maxSum);
if (root->left && root->right){
maxSum = max(maxSum, leftSubTree + rightSubTree + root->data);
return max(leftSubTree, rightSubTree) + root->data;
}
return (!root->left)? rightSubTree + root->data: leftSubTree + root->data;
}
int main(){
struct Node *root = insertNode(-2);
root->left = insertNode(6);
root->right = insertNode(4);
root->left->left = insertNode(5);
root->left->right = insertNode(1);
root->left->left->left = insertNode(2);
root->left->left->right = insertNode(-1);
root->left->right->left = insertNode(-3);
root->left->right->left->left = insertNode(7);
root->right->left = insertNode(9);
root->right->right = insertNode(3);
int maxSum = INT_MIN;
maxPathSumLeaf(root, maxSum);
cout<<"Max pathSum of between two leaf nodes for the given binary tree is "<<maxSum;
return 0;
} আউটপুট
Max pathSum of between two leaf nodes for the given binary tree is 24


