ধরুন আমাদের একটি অ-খালি বাইনারি গাছ আছে। আমাদের পথের যোগফল খুঁজে বের করতে হবে। তাই এখানে, একটি পাথ হল কিছু প্রারম্ভিক নোড থেকে যেকোন নোডের নোডের যেকোন ক্রম যেখানে পিতামাতা-সন্তান সংযোগ রয়েছে। পাথটিতে কমপক্ষে একটি নোড থাকতে হবে এবং রুট নোডের মধ্য দিয়ে যেতে হবে না। তাই যদি ইনপুট ট্রি হয় −
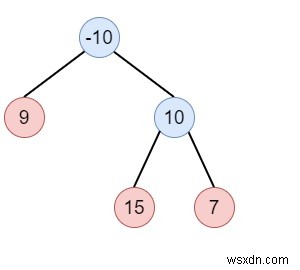
এখানে আউটপুট হবে 32।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
সমাধান() নামক একটি পদ্ধতি সংজ্ঞায়িত করুন, এটি নোড গ্রহণ করবে
-
যদি নোড নাল হয় বা নোডের মান 0 হয়, তাহলে 0
ফেরত দিন -
left :=0 এর সর্বোচ্চ এবং সমাধান (নোডের বামে)
-
ডান :=সর্বোচ্চ 0 এবং সমাধান (নোডের ডানদিকে)
-
উত্তর :=উত্তরের সর্বোচ্চ এবং বাম + ডান + নোডের ডেটা
-
রিটার্ন নোড ডেটা + বাম এবং ডানের সর্বাধিক
-
মূল পদ্ধতি থেকে, উত্তর সেট করুন :=-inf, তারপর কল সমাধান(root) এবং উত্তর দিন
উদাহরণ
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
class TreeNode:
def __init__(self, data, left = None, right = None):
self.data = data
self.left = left
self.right = right
def insert(temp,data):
que = []
que.append(temp)
while (len(que)):
temp = que[0]
que.pop(0)
if (not temp.left):
if data is not None:
temp.left = TreeNode(data)
else:
temp.left = TreeNode(0)
break
else:
que.append(temp.left)
if (not temp.right):
if data is not None:
temp.right = TreeNode(data)
else:
temp.right = TreeNode(0)
break
else:
que.append(temp.right)
def make_tree(elements):
Tree = TreeNode(elements[0])
for element in elements[1:]:
insert(Tree, element)
return Tree
class Solution(object):
def maxPathSum(self, root):
self.ans = -float('inf')
self.solve(root)
return self.ans
def solve(self,node):
if not node or node.data == 0:
return 0
left = max(0,self.solve(node.left))
right = max(0,self.solve(node.right))
self.ans = max(self.ans,left+right+node.data)
return node.data + max(left,right)
ob = Solution()
root = make_tree([-10,9,10,None,None,15,7])
print(ob.maxPathSum(root)) ইনপুট
[-10,9,10,None,None,15,7]
আউটপুট
32


