এই সমস্যায়, আমাদের একটি বাইনারি ট্রি দেওয়া হয়েছে এবং আমাদের বাইনারি গাছের সমস্ত অভ্যন্তরীণ নোড প্রিন্ট করতে হবে৷
বাইনারী গাছ একটি গাছ যেখানে একটি নোডে সর্বাধিক 2টি চাইল্ড নোড থাকতে পারে। নোড বা শীর্ষবিন্দুতে কোনো নোড থাকতে পারে না, একটি চাইল্ড বা দুটি চাইল্ড নোড।
উদাহরণ −
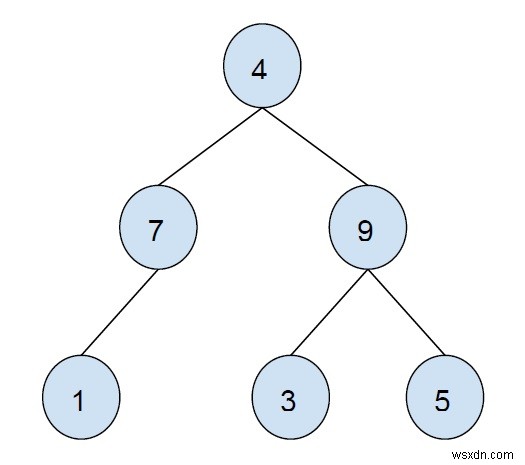
অভ্যন্তরীণ নোড একটি নোড যাতে কমপক্ষে একটি শিশু থাকতে পারে অর্থাৎ নন-লিফ নোড হল একটি অভ্যন্তরীণ নোড৷
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক -
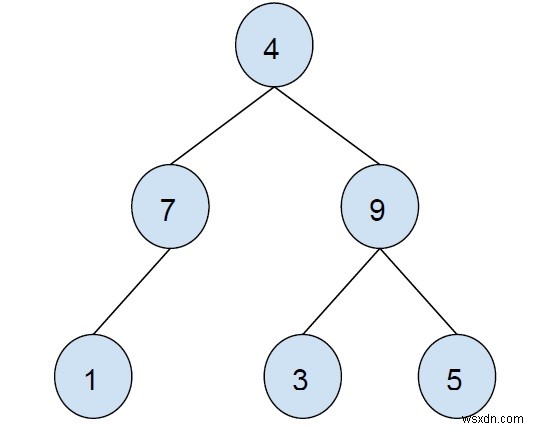
আউটপুট − 7 4 9
এই সমস্যা সমাধানের জন্য, আমরা BFS(প্রস্থ-প্রথম অনুসন্ধান) ট্রাভার্সাল ব্যবহার করে বাইনারি ট্রিটি অতিক্রম করব।
ট্রাভার্সাল করার সময় আমরা নোডগুলিকে একটি সারিতে ঠেলে দেব। যখন আমরা সারি থেকে উপাদানগুলি পপ করি, তখন আমরা গাছের সমস্ত নোড প্রিন্ট করব যেগুলিতে কোনও চাইল্ড নোড নেই৷
উদাহরণ
আমাদের যুক্তি নিচের কোড দ্বারা বাস্তবায়িত হয় −
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node *left, *right;
Node(int data){
left = right = NULL;
this->data = data;
}
};
void printNonLeafNodes(Node* root) {
queue<Node*> treeNodes;
treeNodes.push(root);
while (!treeNodes.empty()) {
Node* curr = treeNodes.front();
treeNodes.pop();
bool isInternal = 0;
if (curr->left) {
isInternal = 1;
treeNodes.push(curr->left);
}
if (curr->right) {
isInternal = 1;
treeNodes.push(curr->right);
}
if (isInternal)
cout<<curr->data<<"\t";
}
}
int main() {
Node* root = new Node(43);
root->left = new Node(12);
root->right = new Node(78);
root->left->left = new Node(4);
root->right->left = new Node(9);
root->right->right = new Node(1);
root->right->right->right = new Node(50);
root->right->right->left = new Node(25);
cout<<"All internal Nodes of the binary tree are :\n";
printNonLeafNodes(root);
return 0;
} আউটপুট
All internal Nodes of the binary tree are − 43 12 78 1


