C++ এ সব গভীরতম নোড সহ সবচেয়ে ছোট সাবট্রি

ধরুন আমাদের একটি বাইনারি ট্রি মূলে প্রোথিত আছে, প্রতিটি নোডের গভীরতা হল রুটের সবচেয়ে কম দূরত্ব। এখানে একটি নোড সবচেয়ে গভীর হয় যদি পুরো গাছের যেকোনো নোডের মধ্যে এটির সম্ভাব্য সর্বাধিক গভীরতা থাকে। একটি নোডের সাবট্রি হল সেই নোড, প্লাস সেই নোডের সমস্ত বংশধরের সেট। আমাদের সবচেয়ে বড় গভীরতা সহ নোডটি খুঁজে বের করতে হবে যাতে এটির সাবট্রিতে সমস্ত গভীরতম নোড থাকে। তাই গাছটি যদি −

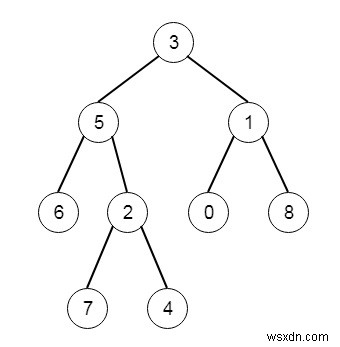
তারপর গভীরতম সাবট্রি হবে −

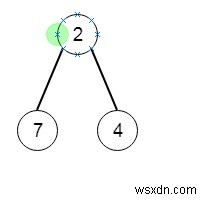
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• সমাধান() নামক একটি পদ্ধতির সংজ্ঞা দিন, এটি ইনপুট হিসাবে রুট হবে

• যদি রুট নাল হয়, তাহলে রিটার্ন করুন (নাল, 0)

• l :=সমাধান (মূলের বামে), r :=সমাধান (মূলের ডানদিকে)

• যদি বামের দ্বিতীয় মান> r এর দ্বিতীয় মান হয়, তাহলে একটি জোড়া ফেরত দিন (l-এর প্রথম, l-এর 1 + সেকেন্ড)

• অন্যথায় যখন বামের দ্বিতীয় মান

• একটি জোড়া ফেরত দিন(মূল, l + 1 এর দ্বিতীয়)

• মূল পদ্ধতি থেকে solve(root) কল করুন এবং এর দ্বিতীয় মান ফেরত দিন

উদাহরণ(C++)

আরো ভালোভাবে বোঝার জন্য নিচের বাস্তবায়নটি দেখি -

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
   public:
      int val;
      TreeNode *left, *right;
      TreeNode(int data){
         val = data;
         left = right = NULL;
      }
   };
   void insert(TreeNode **root, int val){
      queue<TreeNode*> q;
      q.push(*root);
      while(q.size()){
         TreeNode *temp = q.front();
         q.pop();
         if(!temp->left){
            if(val != NULL)
               temp->left = new TreeNode(val);
            else
               temp->left = new TreeNode(0);
            return;
         } else {
            q.push(temp->left);
         }
         if(!temp->right){
            if(val != NULL)
               temp->right = new TreeNode(val);
            else
               temp->right = new TreeNode(0);
            return;
         } else {
            q.push(temp->right);
      }
   }
}
TreeNode *make_tree(vector<int> v){
   TreeNode *root = new TreeNode(v[0]);
   for(int i = 1; i<v.size(); i++){
      insert(&root, v[i]);
   }
   return root;
}
void tree_level_trav(TreeNode*root){
   if (root == NULL) return;
   cout << "[";
   queue<TreeNode *> q;
   TreeNode *curr;
   q.push(root);
   q.push(NULL);
   while (q.size() > 1) {
      curr = q.front();
      q.pop();
      if (curr == NULL){
         q.push(NULL);
      } else {
         if(curr->left)
         q.push(curr->left);
         if(curr->right)
            q.push(curr->right);
         if(curr->val == 0 || curr == NULL){
            cout << "null" << ", ";
         } else {
            cout << curr->val << ", ";
         }
      }
   }
   cout << "]"<<endl;
}
class Solution {
   public:
   pair <TreeNode*, int> solve(TreeNode* root){
      if(!root || root->val == 0) return {NULL, 0};
      pair <TreeNode*, int> L = solve(root->left);
      pair <TreeNode*, int> R = solve(root->right);
      if(L.second > R.second)return {L.first, L.second + 1};
      else if(L.second < R.second) return {R.first, R.second + 1};
      return {root, L.second + 1};
   }
   TreeNode* subtreeWithAllDeepest(TreeNode* root) {
      return solve(root).first;
   }
};
main(){
   vector<int> v = {3,5,1,6,2,0,8,NULL,NULL,7,4};
   TreeNode *root = make_tree(v);
   Solution ob;
   tree_level_trav(ob.subtreeWithAllDeepest(root)) ;
}

ইনপুট

{3,5,1,6,2,0,8,NULL,NULL,7,4}

আউটপুট

[2,7,4]