C++ এ সমস্ত সম্ভাব্য সম্পূর্ণ বাইনারি গাছ

ধরুন একটি সম্পূর্ণ বাইনারি ট্রি হল একটি বাইনারি ট্রি যেখানে প্রতিটি নোডে ঠিক 0 বা 2টি শিশু রয়েছে৷ তাই আমাদের এন নোড সহ সম্ভাব্য সমস্ত বাইনারি গাছের একটি তালিকা খুঁজে বের করতে হবে। উত্তরের প্রতিটি গাছের প্রতিটি নোডে অবশ্যই node.val =0 থাকতে হবে। প্রত্যাবর্তিত গাছ যে কোনো ক্রমে হতে পারে। সুতরাং যদি ইনপুট 7 হয়, তাহলে গাছগুলি হল −

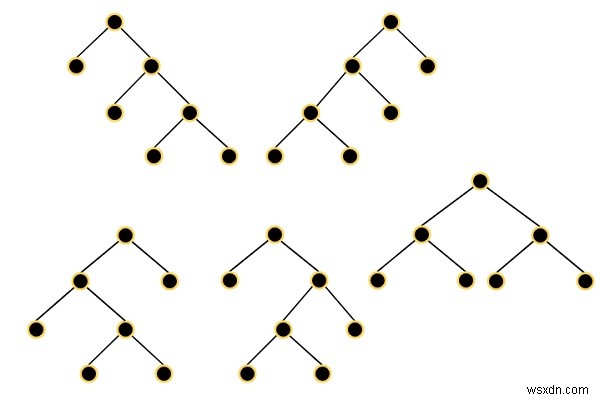
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• পূর্ণসংখ্যা টাইপ কী এবং ট্রি টাইপ মানের একটি মানচিত্র m সংজ্ঞায়িত করুন।

• allPossibleFBT() নামে একটি পদ্ধতি সংজ্ঞায়িত করুন, এটি ইনপুট হিসাবে N গ্রহণ করবে

• N হল 1, তারপর একটি নোড সহ একটি ট্রি তৈরি করুন যার মান 0, এবং ফিরে আসুন

• যদি m-এর কী N থাকে, তাহলে m[N] ফেরত দিন  temp, এবং req নামক একটি অ্যারে নির্ধারণ করুন :=N – 1

• রেঞ্জ 1 থেকে অনুরোধ – 1

  -এর মধ্যে বাম জন্য

  • ডান:=অনুরোধ – বাম

  • যদি বাম =2 বা ডান =2, তাহলে পরবর্তী পুনরাবৃত্তির জন্য যান

  • leftPart :=allPossibleFBT(বামে), rightPart :=allPossibleFBT(ডান)

  • j এর জন্য রেঞ্জ 0 থেকে বাম অংশ - 1

    এর আকার

    • k এর জন্য রেঞ্জ 0 থেকে rightPart – 1

      এর আকার

      • root :=মান 0

        সহ একটি নতুন নোড

      • মূলের বাম :=বাম অংশ[জে], মূলের ডানদিকে :=ডানভাগ[কে]

      • উত্তরে রুট সন্নিবেশ করান

• সেট m[N] :=ans এবং রিটার্ন।

উদাহরণ(C++)

আরো ভালোভাবে বোঝার জন্য নিচের বাস্তবায়নটি দেখি -

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
   public:
      int val;
      TreeNode *left, *right;
      TreeNode(int data){
         val = data;
         left = right = NULL;
      }
};
void tree_level_trav(TreeNode*root){
   if (root == NULL) return;
      cout << "[";
   queue<TreeNode *> q;
   TreeNode *curr;
   q.push(root);
   q.push(NULL);
   while (q.size() > 1) {
      curr = q.front();
      q.pop();
      if (curr == NULL){
         q.push(NULL);
      } else {
            if(curr->left)
               q.push(curr->left);
            if(curr->right)
               q.push(curr->right);
            if(curr == NULL || curr->val == 0){
               cout << "null" << ", ";
            } else {
            cout << curr->val << ", ";
         }
      }
   }
   cout << "]"<<endl;
}
class Solution {
   public:
   map < int, vector <TreeNode*> > m;
   vector<TreeNode*> allPossibleFBT(int N) {
      if(N == 1){
         vector <TreeNode*> temp;
         TreeNode *n = new TreeNode(1);
         n->left = new TreeNode(0);
         n->right = new TreeNode(0);
         temp.push_back(n);
         return temp;
      }
      if(m.count(N))return m[N];
      vector <TreeNode*> ans;
      int required = N - 1;
      for(int left = 1; left < required; left++){
         int right = required - left;
         if(left == 2 || right == 2)continue;
         vector <TreeNode*> leftPart = allPossibleFBT(left);
         vector <TreeNode*> rightPart = allPossibleFBT(right);
         for(int j = 0; j < leftPart.size(); j++){
            for(int k = 0; k < rightPart.size(); k++){
               TreeNode* root = new TreeNode(1);
               root->left = leftPart[j];
               root->right = rightPart[k];
               ans.push_back(root);
            }
         }
      }
      return m[N] = ans;
   }
};
main(){
   vector<TreeNode*> v;
   Solution ob;
   v = (ob.allPossibleFBT(7)) ;
   for(TreeNode *t : v){
      tree_level_trav(t);
   }
}

ইনপুট

7

আউটপুট

[1, 1, 1, null, null, 1, 1, null, null, 1, 1, null, null, null, null, ]
[1, 1, 1, null, null, 1, 1, 1, 1, null, null, null, null, null, null, ]
[1, 1, 1, 1, 1, 1, 1, null, null, null, null, null, null, null, null, ]
[1, 1, 1, 1, 1, null, null, null, null, 1, 1, null, null, null, null, ]
[1, 1, 1, 1, 1, null, null, 1, 1, null, null, null, null, null, null, ]