C++ এ থ্রেশহোল্ড দূরত্বে সবচেয়ে কম সংখ্যক প্রতিবেশীর সাথে শহরটি খুঁজুন

ধরুন 0 থেকে n-1 পর্যন্ত n শহর আছে। যদি আমাদের অ্যারে প্রান্ত থাকে যেখানে প্রান্তগুলি [i] =[fromi, toi, weighti] শহর fromi এবং toi এর মধ্যে একটি দ্বিমুখী এবং ওজনযুক্ত প্রান্তকে প্রতিনিধিত্ব করে এবং পূর্ণসংখ্যা দূরত্বের থ্রেশহোল্ড দেওয়া হয়। আমাদেরকে এমন শহর খুঁজে বের করতে হবে যেগুলির মধ্যে সবচেয়ে কম সংখ্যক শহর কোনো পথ দিয়ে পৌঁছানো যায় এবং যার দূরত্ব সবচেয়ে বেশি দূরত্বের থ্রেশহোল্ডে, যদি এরকম একাধিক শহর থাকে, তাহলে সবচেয়ে বেশি সংখ্যা দিয়ে শহরটিকে ফেরত দিন৷

তাই যদি ইনপুট −

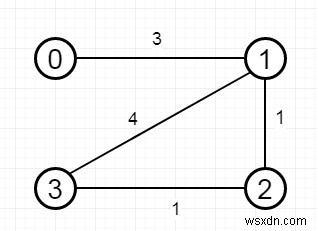
n হল 4 এবং দূরত্ব থ্রেশহোল্ডও 4, তাহলে আউটপুট হবে 3। এর কারণ −

প্রতিবেশী শহরগুলি দূরত্বের প্রান্তিকে =4 প্রতিটি শহরের জন্য −

C0 -> [C1, C2]
C1 -> [C0, C2, C3]
C2 -> [C0, C1, C3]
C3 -> [C1, C2]

শহর 0 এবং 3 এর দূরত্বের থ্রেশহোল্ডে 2টি প্রতিবেশী শহর আছে =4, কিন্তু আমাদেরকে শহর 3 ফিরতে হবে কারণ এটির সংখ্যা সবচেয়ে বেশি।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• dp নামক ক্রম n x n এর একটি বর্গ ম্যাট্রিক্স সংজ্ঞায়িত করুন এবং এটিকে অসীম দিয়ে পূরণ করুন

• গ্রাফের সংলগ্ন ম্যাট্রিক্স (কস্ট ম্যাট্রিক্স) তৈরি করুন এবং dp এ সঞ্চয় করুন

• ret :=0 এবং cnt :=infinity

• k এর জন্য 0 থেকে n – 1

  পরিসরে

  • 0 থেকে n – 1

    রেঞ্জের i জন্য

    • j-এর জন্য 0 থেকে n – 1

      পরিসরে

      • যদি i =j, তাহলে পরবর্তী পুনরাবৃত্তির জন্য যান

      • যদি dp[i, j]> dp[i, k] + dp[k, j] হয়, তাহলে

        • dp[j, i] :=dp[i, k] + dp[k, j]

        • dp[i, j] :=dp[i, k] + dp[k, j]

• 0 থেকে n - 1

  রেঞ্জের i জন্য

  • তাপমাত্রা :=0

  • j-এর জন্য 0 থেকে n – 1

    পরিসরে

    • temp :=temp + 1 যখন dp[i, j] <=t, অন্যথায় তাপমাত্রা একই থাকে

  • যদি temp <=cnt, তাহলে cnt :=temp এবং ret :=i

• রিটার্ন রিটার্ন

উদাহরণ (C++)

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
   int findTheCity(int n, vector<vector<int>>& e, int t) {
      vector < vector <int> > dp(n, vector <int>(n, 1e7));
      for(int i = 0; i < e.size(); i++){
         int u = e[i][0];
         int v = e[i][1];
         int w = e[i][2];
         dp[u][v] = w;
         dp[v][u] = w;
      }
      int ret = 0;
      int cnt = INT_MAX;
      for(int k = 0; k < n; k++){
         for(int i = 0; i < n; i++){
            for(int j = 0; j < n; j++){
               if(i == j) continue;
               if(dp[i][j] > dp[i][k] + dp[k][j]){
                  dp[j][i] = dp[i][j] = (dp[i][k] + dp[k][j]);
               }
            }
         }
      }
      for(int i = 0; i < n; i++){
         int temp = 0;
         for(int j = 0; j < n; j++){
            temp += (dp[i][j] <= t);
         }
         if(temp <= cnt){
            cnt = temp;
            ret = i;
         }
      }
      return ret;
   }
};
main(){
   vector<vector<int>> v = {{0,1,3},{1,2,1},{1,3,4},{2,3,1}};
   Solution ob;
   cout << (ob.findTheCity(4, v, 4));
}

ইনপুট

4
[[0,1,3],[1,2,1],[1,3,4],[2,3,1]]
4

আউটপুট

3