একটি ভারসাম্যপূর্ণ BST-তে একটি ট্রিপলেট আছে কিনা তা খুঁজুন যা C++ এ শূন্য যোগ করে

ধরুন আমাদের একটি ভারসাম্যপূর্ণ বাইনারি সার্চ ট্রি আছে, আমাদেরকে is_valid_triplet() নামে একটি ফাংশন তৈরি করতে হবে যা প্রদত্ত BST-তে একটি ট্রিপলেট থাকলে সত্য ফেরত দেয় যার যোগফল 0 এর সমান হয়, অন্যথায় মিথ্যা ফেরত দেয় . এই সীমাবদ্ধতাগুলি অনুসরণ করে পদ্ধতিটি ডিজাইন করুন -

প্রত্যাশিত সময়ের জটিলতা হল O(n^2)
O(logn) অতিরিক্ত স্থান ব্যবহার করা যেতে পারে।

সুতরাং, যদি ইনপুটটি এরকম হয়

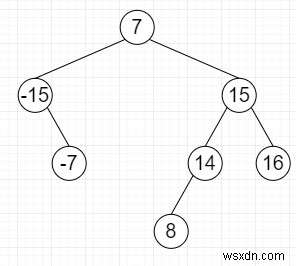
তাহলে আউটপুট হবে True, যেমন ট্রিপলেট হল [-15,7,8]

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

একটি ফাংশন সংজ্ঞায়িত করুন bst_to_doubli_list(), এটি রুট, মাথা, পুচ্ছ,
যদি রুট NULL এর মত হয়, তাহলে −
- ফেরত
যদি মূলের বাম অংশ শূন্য না হয়, তাহলে −
- bst_to_doubli_list(মূলের বাম, মাথা, লেজ)
মূলের বাম:=লেজ
যদি লেজ শূন্য না হয়, তাহলে −
- লেজের ডানদিকে :=মূল
অন্যথায়
- head :=root
লেজ :=মূল
যদি মূলের ডানদিকে শূন্য না হয়, তাহলে −
- bst_to_doubli_list(মূলের ডানদিকে, মাথা, পুচ্ছ)
একটি ফাংশন is_in_double_list() সংজ্ঞায়িত করুন, এটি মাথা, লেজ, যোগফল,
যখন মাথা লেজের সমান না হয়, −
করুন
- বর্তমান :=মাথার চাবি + লেজের চাবি
- যদি বর্তমান যোগফলের সমান হয়, তাহলে −
  - প্রত্যাবর্তন সত্য
- অন্যথায় যখন বর্তমান> যোগফল, তারপর −
  - পুচ্ছ :=লেজের বাম
- অন্যথায়
  - মাথা :=মাথার ডানদিকে
মিথ্যা ফেরত দিন
প্রধান পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন -
যদি মূল শূন্য হয়, তাহলে −
- মিথ্যা ফেরত দিন
মাথা =শূন্য
পুচ্ছ =শূন্য
bst_to_doubli_list(মূল, মাথা, পুচ্ছ)
যখন (মাথার ডানদিকে লেজ এবং মাথার চাবির সমান নয় <0), −
করুন
- যদি_দ্বিতীয় হয় (মাথার ডানদিকে, লেজ, মাথার চাবি * (-1), তাহলে
  - প্রত্যাবর্তন সত্য
- অন্যথায়
  - মাথা :=মাথার ডানদিকে
মিথ্যা ফেরত দিন

উদাহরণ (C++)

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

#include <bits/stdc++.h>
using namespace std;
class TreeNode {
   public:
   int key;
   TreeNode *left;
   TreeNode *right;
   TreeNode() : key(0), left(NULL), right(NULL) {}
   TreeNode(int x) : key(x), left(NULL), right(NULL) {}
};
void bst_to_doubli_list(TreeNode* root, TreeNode** head, TreeNode** tail) {
   if (root == NULL)
      return;
   if (root->left)
      bst_to_doubli_list(root->left, head, tail);
   root->left = *tail;
   if (*tail)
      (*tail)->right = root;
   else
      *head = root;
      *tail = root;
   if (root->right)
      bst_to_doubli_list(root->right, head, tail);
}
bool is_in_double_list(TreeNode* head, TreeNode* tail, int sum) {
   while (head != tail) {
      int current = head->key + tail->key;
      if (current == sum)
         return true;
      else if (current > sum)
         tail = tail->left;
      else
         head = head->right;
   }
   return false;
}
bool is_valid_triplet(TreeNode *root) {
   if (root == NULL)
      return false;
   TreeNode* head = NULL;
   TreeNode* tail = NULL;
   bst_to_doubli_list(root, &head, &tail);
   while ((head->right != tail) && (head->key < 0)){
      if (is_in_double_list(head->right, tail, -1*head->key))
         return true;
      else
         head = head->right;
   }
   return false;
}
TreeNode* insert(TreeNode* root, int key) {
   if (root == NULL)
      return new TreeNode(key);
   if (root->key > key)
      root->left = insert(root->left, key);
   else
      root->right = insert(root->right, key);
   return root;
}
int main(){
   TreeNode* root = NULL;
   root = insert(root, 7);
   root = insert(root, -15);
   root = insert(root, 15);
   root = insert(root, -7);
   root = insert(root, 14);
   root = insert(root, 16);
   root = insert(root, 8);
   cout << is_valid_triplet(root);
}

ইনপুট

root = insert(root, 7);
root = insert(root, -15);
root = insert(root, 15);
root = insert(root, -7);
root = insert(root, 14);
root = insert(root, 16);
root = insert(root, 8);