পাইথনের উৎস থেকে k-এর বেশি দৈর্ঘ্যের পথ আছে কিনা তা খুঁজুন

ধরুন আমাদের একটি গ্রাফ আছে, আমাদের একটি উৎস শীর্ষবিন্দু এবং একটি সংখ্যা k আছে। k হল উৎস থেকে গন্তব্যের মধ্যে গ্রাফের পথের দৈর্ঘ্য, আমাদের পরীক্ষা করতে হবে যে আমরা উৎস থেকে শুরু করে অন্য কোনো শীর্ষে (গন্তব্য হিসাবে) শেষ হওয়া একটি সরল পথ (চক্র ছাড়া) খুঁজে পাব কিনা। গ্রাফটি নিম্নলিখিত −

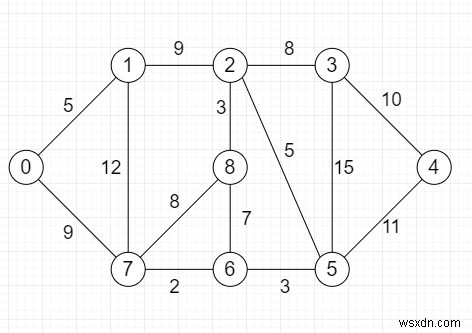
সুতরাং, যদি ইনপুটটি Source =0, k =64 এর মত হয়, তাহলে আউটপুটটি True হবে কারণ সেখানে একটি সহজ পথ 0 থেকে 7 থেকে 1 থেকে 2 থেকে 8 থেকে 6 থেকে 5 থেকে 3 থেকে 4 পর্যন্ত বিদ্যমান, এই পথের দৈর্ঘ্য মোট 68 এর দূরত্ব যা 64 এর বেশি।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• অর্ডার নোড x নোডের সংলগ্নতা ম্যাট্রিক্স অ্যাডজ ব্যবহার করে গ্রাফটি সংজ্ঞায়িত করুন এবং প্রান্ত খরচ দিয়ে পূরণ করুন

• একটি ফাংশন সমাধান () সংজ্ঞায়িত করুন। এটি উৎস, কে, পথ

  গ্রহণ করবে

• যদি k <=0, তাহলে

  • রিটার্ন ট্রু

• i :=0

• যখন আমি adj[উৎস] এর আকারের সমান নই, তাই করুন

  • v :=adj[source, i, 0]

  • w :=adj[source, i, 1]

  • i :=i + 1

  • যদি পাথ[v] সত্য হয়, তাহলে

    • পরবর্তী পুনরাবৃত্তির জন্য যান

  • যদি w>=k, তাহলে

    • রিটার্ন ট্রু

  • পথ[v] :=সত্য

  • যদি সমাধান (v, k-w, path) সত্য হয়, তাহলে

    • রিটার্ন ট্রু

  • পথ[v] :=মিথ্যা

• রিটার্ন ফলস

• প্রধান পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন -

• পথ :=নোডের মতো আকারের একটি তালিকা, তারপর মিথ্যা মান দিয়ে পূরণ করুন

• পথ [সূত্র] :=1

• রিটার্ন সলভ (উৎস, কে, পথ)

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

class Graph:
   def __init__(self, nodes):
      self.nodes = nodes
      self.adj = [[] for i in range(nodes)]
   def insert_edge(self,u, v, w):
      self.adj[u].append([v, w])
      self.adj[v].append([u, w])
   def solve(self,source, k, path):
      if (k <= 0):
         return True
      i = 0
      while i != len(self.adj[source]):
         v = self.adj[source][i][0]
         w = self.adj[source][i][1]
         i += 1
         if (path[v] == True):
            continue
         if (w >= k):
            return True
         path[v] = True
         if (self.solve(v, k-w, path)):
            return True
         path[v] = False
      return False
   def is_there_any_path(self,source, k):
      path = [False]*self.nodes
      path[source] = 1
      return self.solve(source, k, path)

nodes = 9
g = Graph(nodes)
g.insert_edge(0, 1, 5)
g.insert_edge(0, 7, 9)
g.insert_edge(1, 2, 9)
g.insert_edge(1, 7, 12)
g.insert_edge(2, 3, 8)
g.insert_edge(2, 8, 3)
g.insert_edge(2, 5, 5)
g.insert_edge(3, 4, 10)
g.insert_edge(3, 5, 15)
g.insert_edge(4, 5, 11)
g.insert_edge(5, 6, 3)
g.insert_edge(6, 7, 2)
g.insert_edge(6, 8, 7)
g.insert_edge(7, 8, 8)
source = 0
k = 64
print(g.is_there_any_path(source, k))

ইনপুট

nodes = 9
g = Graph(nodes)
g.insert_edge(0, 1, 5)
g.insert_edge(0, 7, 9)
g.insert_edge(1, 2, 9)
g.insert_edge(1, 7, 12)
g.insert_edge(2, 3, 8)
g.insert_edge(2, 8, 3)
g.insert_edge(2, 5, 5)
g.insert_edge(3, 4, 10)
g.insert_edge(3, 5, 15)
g.insert_edge(4, 5, 11)
g.insert_edge(5, 6, 3)
g.insert_edge(6, 7, 2)
g.insert_edge(6, 8, 7)
g.insert_edge(7, 8, 8)
source = 0
k = 64

আউটপুট

True