একটি বিন্দুর ঘূর্ণন C++ এ অন্য একটি বিন্দুতে

উৎপত্তি সম্পর্কে X বিন্দুর ঘূর্ণন ঘড়ির কাঁটার বিপরীত দিকে একটি কোণ θ দ্বারা করা হয় −

X by θ উৎপত্তি সম্পর্কে অ্যান্টি-clRotateockwise:X*polar( 1.0,θ)।

এখানে, জটিল সংখ্যাগুলির জন্য পোলার ফাংশনটি হেডার ফাইলের অধীনে সংজ্ঞায়িত করা হয়েছে এবং ফেজ এঙ্গেল ব্যবহার করে একটি জটিল সংখ্যা খুঁজে বের করতে ব্যবহৃত হয় এবং magnitude.polar(mag, angle) একটি জটিল সংখ্যা প্রদান করে।

একটি বিন্দু Y সম্পর্কে X বিন্দুর ঘূর্ণন

একটি বিন্দুকে অন্য বিন্দুতে ঘোরানোর জন্য, আমরা অনুবাদ ব্যবহার করব যেখানে সমস্ত স্থানাঙ্কের গতিবিধি একটি নির্দিষ্ট দিকে ঘটে।

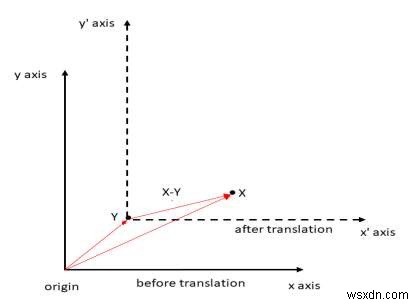
X কে Y সম্পর্কে ঘোরানোর ধাপ।

• X থেকে Y অনুবাদ করুন, তাই Y নতুন উৎপত্তি হয়ে ওঠে। এটি সমস্ত বিন্দু থেকে Y বিয়োগ করে করা যেতে পারে। X এখন X-Y হয়৷

  ৷

• উপরের সূত্র ব্যবহার করে নতুন উৎপত্তি সম্পর্কে (X-Y) ঘোরান:(X-Y)*polar( 1.0,θ )

• সমস্ত পয়েন্টে Y যোগ করে ব্যাক-অনুবাদ।

Y সম্পর্কে X-এর ঘূর্ণন হল :(X-Y)*পোলার(1.0,θ ) + Y

নীচে অন্য বিন্দু সম্পর্কে বিন্দুর ঘূর্ণন প্রদর্শন করার কোড রয়েছে

উদাহরণ

#include <iostream>
#include <complex>
using namespace std;
typedef complex<double> point;
#define x real()
#define y imag()
int main(){
   // Rotate P about Q
   point X(5.0, 3.0);
   point Y(2.0, 4.0);
   // Angle of rotation is 90 degrees
   double theta = 3.14/2;
   point Xnew=(X-Y) * polar(1.0, theta) + Y;
   cout << "rotating X 90 degrees anti-clockwise about Y becomes:";
   cout << "(" << Xnew.x << ", " << Xnew.y << ")" << endl;
   return 0;
}

আউটপুট

rotating X 90 degrees anti-clockwise about Y becomes:(3.00239, 6.9992)