এই সমস্যায়, আমাদের একটি 2-D সমতলে একটি বিন্দু P দেওয়া হয়েছে এবং পয়েন্টগুলি a, b, cof সমীকরণ ax + by + c =0 দেওয়া হয়েছে। আমাদের কাজ হল খুঁজে বের করা একটি পয়েন্টিন 2-ডি সমতলের একটি আয়না চিত্র।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট
P = (2, 1), a = 1, b = -1, c = 0
আউটপুট
(1, 2)
ব্যাখ্যা
প্লেনটি দেখে মনে হচ্ছে,
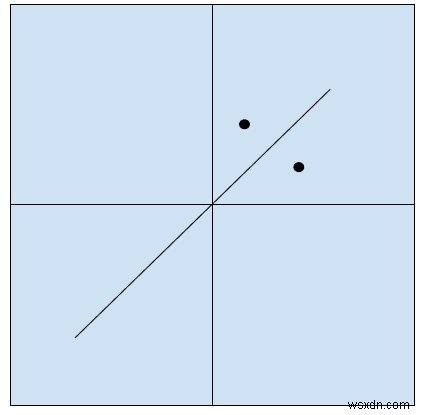
সমাধান পদ্ধতি
সমস্যা সমাধানের জন্য, আমাদের স্থানাঙ্ক (x', y') সহ সমীকরণ বিন্দু P' খুঁজে বের করতে হবে। সুতরাং, আমাদের কাছে রয়েছে R, মধ্যবিন্দু যেখানে লাইন ফর্ম P - P' মিরর লাইনকে ছেদ করে।
P-R-P' রেখাটি আয়নার লম্ব। তাই, রেখার সমীকরণ হবে,
ay - by + d = 0
বিন্দুগুলি হল P(x, y); P'(x', y'); R(xm, ym)।
বিন্দু P এবং R পরিচিত। সুতরাং, সমীকরণ ব্যবহার করে আমরা P’ কে,
হিসেবে পাব$$\left(\frac{??'-??}{??}\right)=\left(\frac{??'-??}{??} \right)=\left(\frac{ ????-????+??}{??^2+x^2}\right)$$
আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম,
উদাহরণ
#include <iostream>
using namespace std;
void findMirrorImage( double a, double b, double c, double x, double y){
double points = -2 * (a * x + b * y + c) / (a * a + b * b);
double xm = points * a + x;
double ym = points * b + y;
cout<<"("<<xm<<","<<ym<<")";
}
int main(){
double a = -1.0;
double b = 1.0;
double c = 0.0;
double x = 1.0;
double y = 0.0;
cout<<"Image of point ("<<x<<", "<<y<<") using mirror ("<<a<<")x + ("<<b<<")y + ("<<c<< ") = 0, is :";
findMirrorImage(a, b, c, x, y);
return 0;
} আউটপুট
Image of point (1, 0) using mirror (-1)x + (1)y + (0) = 0, is :(0,1)


