একটি মান 'n' দিয়ে দেওয়া হয়েছে এবং কাজটি হল n-এর জন্য কেন্দ্রীভূত অনাভুজ সংখ্যা এবং n পর্যন্ত কেন্দ্রীভূত অনাগোনাল সিরিজ তৈরি করা এবং ফলাফলগুলি প্রদর্শন করা৷
কেন্দ্রিক অনাভুজ সংখ্যা কী?
কেন্দ্রীভূত অনাগোনাল সংখ্যার মধ্যে বিন্দু দ্বারা গঠিত অনাগোনাল স্তর থাকে এবং কেন্দ্রে একটি সংশ্লিষ্ট বিন্দু থাকে।
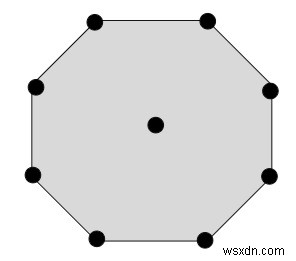
উপরে কেন্দ্রীভূত অনাভুজাকার সংখ্যার চিত্র দেওয়া হল 𝑁2। এটি সূত্র ব্যবহার করে গণনা করা যেতে পারে −
$$Nc(n)=\frac{(3n-2)(3n-1)}{2}$$
ইনপুট
number: 20
আউটপুট
centered nonagonal number : 1711
ইনপুট
number: 10
আউটপুট
centered nonagonal series : 1 10 28 55 91 136 190 253 325 406
অ্যালগরিদম
Start Step 1→ declare function to calculate centered nonagonal number int calculate_number(int num) return (3 * num - 2) * (3 * num - 1) / 2 Step 2→ declare function to calculate centered nonagonal series int calculate_series(int num) Loop For int i = 1and i <= num and i++ Print (3 * i - 2) * (3 * i - 1) / 2 End Step 3→ In main() Declare int num = 20 Call calculate_number(num) Declare num = 10 Call calculate_series(num) Stop
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
//calculate centered nonagonal number
int calculate_number(int num){
return (3 * num - 2) * (3 * num - 1) / 2;
}
int calculate_series(int num){
for (int i = 1; i <= num; i++){
cout << (3 * i - 2) * (3 * i - 1) / 2;
cout << " ";
}
}
int main(){
int num = 20;
cout<<"centered nonagonal number : "<<calculate_number(num)<<endl;
num = 10;
cout<<"centered nonagonal series : ";
calculate_series(num);
return 0;
} আউটপুট
উপরের কোডটি চালালে এটি নিম্নলিখিত আউটপুট −
উৎপন্ন করবেcentered nonagonal number : 1711 centered nonagonal series : 1 10 28 55 91 136 190 253 325 406


