C++ এ দুটি ভিন্ন ভাল নোডের যেকোনো জোড়ার মধ্যে সবচেয়ে কম দূরত্ব খুঁজুন

ধরুন আমাদের একটি প্রদত্ত ওয়েটেড আনডিরেক্টেড গ্রাফ রয়েছে যার সাথে N বিভিন্ন নোড এবং M প্রান্ত রয়েছে, কিছু নোড ভাল নোড। আমাদের দুটি ভিন্ন ভাল নোডের যেকোনো জোড়ার মধ্যে সবচেয়ে কম দূরত্ব খুঁজে বের করতে হবে। প্রদত্ত ডায়াগ্রামে নিম্নলিখিত গ্রাফের হলুদটিকে ভাল নোড হিসাবে বিবেচনা করা হয়।

সুতরাং, যদি ইনপুট মত হয়

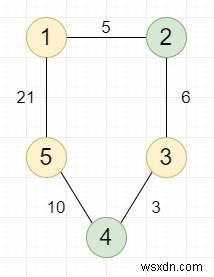
তাহলে আউটপুট হবে 11, যেমন ভালো নোডের জোড়া এবং তাদের মধ্যে দূরত্ব হল:(1 থেকে 3) দূরত্ব হল 11, (3 থেকে 5) দূরত্ব হল 13, (1 থেকে 5) দূরত্ব হল 24, আউট যার মধ্যে 11টি সর্বনিম্ন৷

৷

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

N :=100005
MAX_VAL :=99999999
একটি অগ্রাধিকার সারি তৈরি করুন q
ফলাফল :=MAX_VAL
আরম্ভ করার জন্য i :=1, যখন i <=n, আপডেট করুন (i 1 দ্বারা বাড়ান), করবেন −
- যদি গুড_ভার্ট[i] মিথ্যা হয়, তাহলে -
  - নিম্নলিখিত অংশ উপেক্ষা করুন, পরবর্তী পুনরাবৃত্তি এড়িয়ে যান
- j শুরু করার জন্য :=1, যখন j <=n, আপডেট করুন (j 1 দ্বারা বৃদ্ধি করুন), করুন −
  - dist[j] :=MAX_VAL
  - vis[j] :=0
- dist[i] :=0
- যখন (q খালি নয়), −
  করুন
  - q
    থেকে উপাদান মুছুন
- q
  -এ { 0, i } ঢোকান
- ভাল :=0
- যখন (q খালি নয়), −
  করুন
  - v :=q
    এর শীর্ষ উপাদান
  - q
    থেকে উপাদান মুছুন
  - যদি vis[v] সত্য হয়, তাহলে -
    - নিম্নলিখিত অংশ উপেক্ষা করুন, পরবর্তী পুনরাবৃত্তি এড়িয়ে যান
  - vis[v] :=1
  - good :=good + (1 যখন good_verts[v] সত্য হয়, অন্যথায় 0)
  - যদি dist[v]> ফলাফল হয়, তাহলে −
    - লুপ থেকে বেরিয়ে আসুন
  - ভালো যদি 2 এবং good_verts[v] এর মত হয়, তাহলে −
    - ফলাফল :=ন্যূনতম ফলাফল এবং dist[v]
    - লুপ থেকে বেরিয়ে আসুন
  - j শুরু করার জন্য :=0, যখন j <গ্রাফের আকার[v], আপডেট করুন (j 1 দ্বারা বৃদ্ধি করুন), করুন −
    - থেকে :=গ্রাফ[v, j]।প্রথম
    - ওজন :=গ্রাফ[v, j].সেকেন্ড
    - যদি dist[v] + ওজন
      - dist[to] :=dist[v] + ওজন
      - q
        -এ { dist[to], to } ঢোকান
ফেরত ফলাফল

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

#include <bits/stdc++.h>
using namespace std;
#define N 100005
#define MAX_VAL 99999999
void insert_edge(vector<pair<int, int> > graph[], int x, int y, int weight) {
   graph[x].push_back({ y, weight });
   graph[y].push_back({ x, weight });
}
int get_min_dist(vector<pair<int, int> > graph[], int n, int dist[], int vis[], int good_verts[], int k) {
   priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int>>> q;
   int result = MAX_VAL;
   for (int i = 1; i <= n; i++) {
      if (!good_verts[i])
         continue;
      for (int j = 1; j <= n; j++) {
         dist[j] = MAX_VAL;
         vis[j] = 0;
      }
      dist[i] = 0;
      while (!q.empty())
      q.pop();
      q.push({ 0, i });
      int good = 0;
      while (!q.empty()) {
         int v = q.top().second;
         q.pop();
         if (vis[v])
         continue;
         vis[v] = 1;
         good += good_verts[v];
         if (dist[v] > result)
            break;
         if (good == 2 and good_verts[v]) {
            result = min(result, dist[v]);
            break;
         }
         for (int j = 0; j < graph[v].size(); j++) {
            int to = graph[v][j].first;
            int weight = graph[v][j].second;
            if (dist[v] + weight < dist[to]) {
               dist[to] = dist[v] + weight;
               q.push({ dist[to], to });
            }
         }
      }
   }
   return result;
}
int main() {
   int n = 5, m = 5;
   vector<pair<int, int> > graph[N];
   insert_edge(graph, 1, 2, 3);
   insert_edge(graph, 1, 2, 3);
   insert_edge(graph, 2, 3, 4);
   insert_edge(graph, 3, 4, 1);
   insert_edge(graph, 4, 5, 8);
   int k = 3;
   int good_verts[N], vis[N], dist[N];
   good_verts[1] = good_verts[3] = good_verts[5] = 1;
   cout << get_min_dist(graph, n, dist, vis, good_verts, k);
}

ইনপুট

n = 5, m = 5
insert_edge(graph, 1, 2, 3);
insert_edge(graph, 1, 2, 3);
insert_edge(graph, 2, 3, 4);
insert_edge(graph, 3, 4, 1);
insert_edge(graph, 4, 5, 8);
k = 3
good_verts[1] = good_verts[3] = good_verts[5] = 1;