এই সমস্যায়, আমাদেরকে একটি বাইনারি ট্রি এবং একটি পূর্ণসংখ্যা N দেওয়া হয়েছে। কাজটি হল একটি বাইনারি ট্রির ইনঅর্ডার ট্রাভার্সালে n-ম নোড খুঁজে বের করা।
একটি বাইনারি গাছের একটি বিশেষ শর্ত রয়েছে যে প্রতিটি নোডে সর্বাধিক দুটি শিশু থাকতে পারে৷
ট্রাভার্সাল হল একটি গাছের সমস্ত নোড দেখার প্রক্রিয়া এবং তাদের মানগুলিও প্রিন্ট করতে পারে।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট
N = 6
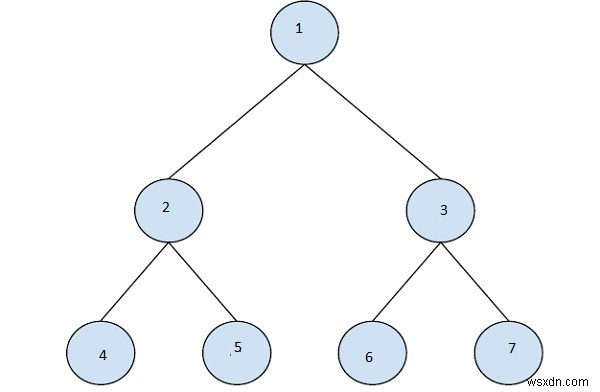
আউটপুট
3
ব্যাখ্যা
inorder traversal of tree : 4, 2, 5, 1, 6, 3, 7
সমাধান পদ্ধতি
ধারণাটি হল বাইনারি ট্রির ইন-অর্ডার ট্রাভার্সাল ব্যবহার করা যা পুনরাবৃত্ত কল ব্যবহার করে করা হয়। প্রতিটি কলে আমরা প্রথমে বাম সাবট্রির জন্য প্রিঅর্ডার() কল করব এবং রুট নোড অতিক্রম করব তারপর প্রিঅর্ডার() কল করব। এই ট্রাভার্সালের সময়, আমরা নোডের সংখ্যা গণনা করব এবং নোডটি প্রিন্ট করব যার জন্য গণনা N।
আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম,
উদাহরণ
#include <iostream>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
struct Node* createNode(int item){
Node* temp = new Node;
temp->data = item;
temp->left = NULL;
temp->right = NULL;
return temp;
}
void findInOrderTraversalRec(struct Node* node, int N){
static int count = 0;
if (node == NULL)
return;
if (count <= N) {
findInOrderTraversalRec(node->left, N);
count++;
if (count == N)
cout<<node->data;
findInOrderTraversalRec(node->right, N);
}
}
int main() {
struct Node* root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
root->right->left = createNode(6);
root->right->right = createNode(7);
int N = 6;
cout<<N<<"th node in inorder traversal is ";
findInOrderTraversalRec(root, N);
return 0;
} আউটপুট
6th node in inorder traversal is 3


