ডেটা স্ট্রাকচারে পরিমার্জিত সময়ের জটিলতা

বিশ্লেষণ পরিত্যাগ করুন

এই বিশ্লেষণটি ব্যবহার করা হয় যখন মাঝে মাঝে অপারেশন খুব ধীর হয়, কিন্তু বেশিরভাগ অপারেশন যা খুব ঘন ঘন সঞ্চালিত হয় দ্রুততর হয়। ডেটা স্ট্রাকচারে আমাদের হ্যাশ টেবিল, ডিসজয়েন্ট সেট ইত্যাদির জন্য পরিমার্জিত বিশ্লেষণ প্রয়োজন।

হ্যাশ-টেবিলে, বেশিরভাগ সময় অনুসন্ধানের সময় জটিলতা হল O(1), কিন্তু কখনও কখনও এটি O(n) অপারেশন চালায়। যখন আমরা বেশিরভাগ ক্ষেত্রে একটি হ্যাশ টেবিলে একটি উপাদান অনুসন্ধান করতে বা সন্নিবেশ করতে চাই তখন এটি কাজটি গ্রহণ করার জন্য ধ্রুবক সময়, কিন্তু যখন একটি সংঘর্ষ ঘটে, তখন সংঘর্ষের রেজোলিউশনের জন্য এটির O(n) বার অপারেশনের প্রয়োজন হয়৷

সমষ্টিগত পদ্ধতি

মোট খরচ বের করতে সমষ্টিগত পদ্ধতি ব্যবহার করা হয়। আমরা যদি একগুচ্ছ ডেটা যোগ করতে চাই, তাহলে আমাদের এই সূত্রের মাধ্যমে পরিমার্জিত খরচ খুঁজে বের করতে হবে।

n ক্রিয়াকলাপগুলির একটি ক্রমের জন্য, খরচ হল −

$\frac{খরচ ( n\:operations)}{n}=\frac{খরচ (সাধারণ\:অপারেশন)+ খরচ (ব্যয়বহুল\:অপারেশন)}{n}$

অমোর্টাইজড বিশ্লেষণের উদাহরণ

একটি গতিশীল অ্যারের জন্য, আইটেমগুলি O(1) সময়ে একটি প্রদত্ত সূচকে সন্নিবেশ করা যেতে পারে। কিন্তু যদি সেই সূচকটি অ্যারেতে উপস্থিত না থাকে তবে এটি ধ্রুবক সময়ের মধ্যে কাজটি করতে ব্যর্থ হয়। সেই ক্ষেত্রে, এটি প্রাথমিকভাবে অ্যারের আকার দ্বিগুণ করে তারপর সূচকটি উপস্থিত থাকলে উপাদানটি সন্নিবেশ করায়।

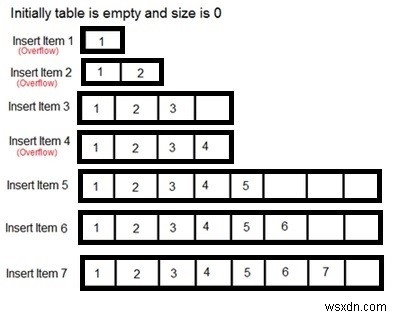
ডায়নামিক অ্যারের জন্য, আসুন ci =ith সন্নিবেশের খরচ।

$So\:ci=1+\begin{cases}i\:-\:1,if\:i-1\:is\:power\:of\:2 \\0, \:\:\:\ :\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:অন্যথায় \end{cases}$

$$\frac{\displaystyle\sum\limits_{i=1}^n ci}{n}\leq\frac{n+\displaystyle\sum\limits_{j=1}^{\lfloor\log{2}{ \lgroup n-1\rgroup}\rfloor} 2j}{n}=\frac{O\lgroup n\rgroup}{n}$$