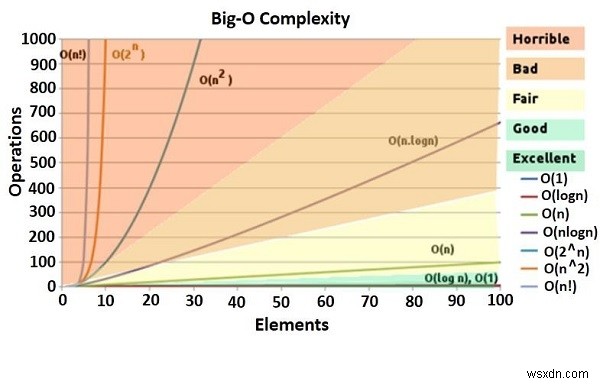
অ্যাসিম্পোটিক বিশ্লেষণ
অ্যাসিম্পোটিক বিশ্লেষণ ব্যবহার করে, আমরা ইনপুট আকারের উপর ভিত্তি করে অ্যালগরিদমের কর্মক্ষমতা সম্পর্কে ধারণা পেতে পারি। আমাদের সঠিক চলমান সময় গণনা করা উচিত নয়, তবে আমাদের চলমান সময় এবং ইনপুট আকারের মধ্যে সম্পর্ক খুঁজে বের করা উচিত। ইনপুটের আকার বাড়ানো হলে আমাদের চলমান সময় অনুসরণ করা উচিত।
স্থান জটিলতার জন্য, আমাদের লক্ষ্য হল অ্যালগরিদম সম্পূর্ণ করার জন্য মূল মেমরিতে কতটা স্থান দখল করা হয়েছে সেই সম্পর্ক বা ফাংশন পাওয়া।
অ্যাসিম্পোটিক আচরণ
একটি ফাংশনের জন্য f(n) অ্যাসিম্পোটিক আচরণ হল f(n) এর বৃদ্ধি যখন n বড় হয়। ছোট ইনপুট মান বিবেচনা করা হয় না. আমাদের কাজ হল ইনপুটের বড় মূল্যের জন্য কতটা সময় লাগবে তা খুঁজে বের করা।
উদাহরণস্বরূপ, f(n) =c * n + k রৈখিক সময় জটিলতা হিসাবে। f(n) =c * n 2 + k হল দ্বিঘাত সময় জটিলতা।
অ্যালগরিদমের বিশ্লেষণকে তিনটি ভিন্ন ক্ষেত্রে ভাগ করা যায়। মামলাগুলি নিম্নরূপ -
সেরা কেস - এখানে চলমান সময়ের নিম্ন সীমা গণনা করা হয়। এটি সর্বোত্তম অবস্থার অধীনে অ্যালগরিদমের আচরণ বর্ণনা করে।
গড় কেস - এই ক্ষেত্রে আমরা অ্যালগরিদমের চলমান সময়ের উপরের এবং নিম্ন সীমার মধ্যে অঞ্চলটি গণনা করি। এই ক্ষেত্রে সম্পাদিত ক্রিয়াকলাপগুলির সংখ্যা সর্বনিম্ন নয় এবং সর্বাধিক নয়৷
৷সবচেয়ে খারাপ কেস - এই ক্ষেত্রে আমরা অ্যালগরিদমের চলমান সময়ের উপরের সীমা গণনা করি। এই ক্ষেত্রে সর্বাধিক সংখ্যক অপারেশন সম্পাদিত হয়।