ডেটা স্ট্রাকচারে সর্বোত্তম বাইনারি অনুসন্ধান গাছ

পূর্ণসংখ্যার একটি সেট সাজানো ক্রমে দেওয়া হয় এবং আরেকটি অ্যারে ফ্রিকোয়েন্সি থেকে ফ্রিকোয়েন্সি গণনা করা হয়। আমাদের কাজ হল সমস্ত অনুসন্ধানের জন্য সর্বনিম্ন খরচ খুঁজে বের করার জন্য সেই ডেটা সহ একটি বাইনারি অনুসন্ধান ট্রি তৈরি করা৷

একটি অক্জিলিয়ারী অ্যারে খরচ[n, n] সাব সমস্যার সমাধান এবং সঞ্চয় করার জন্য তৈরি করা হয়। কস্ট ম্যাট্রিক্স বটম আপ পদ্ধতিতে সমস্যা সমাধানের জন্য ডেটা ধরে রাখবে।

ইনপুট - নোড এবং ফ্রিকোয়েন্সি হিসাবে মূল মান।

Keys = {10, 12, 20}
Frequency = {34, 8, 50}

আউটপুট − সর্বনিম্ন খরচ 142।

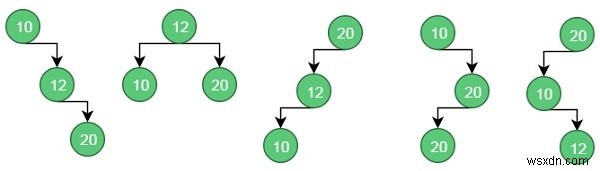
এগুলি প্রদত্ত মান থেকে সম্ভাব্য BST।

কেস 1 এর জন্য, খরচ হল:(34*1) + (8*2) + (50*3) =200

কেস 2 এর জন্য, খরচ হল:(8*1) + (34*2) + (50*2) =176।

একইভাবে, কেস 5 এর জন্য, খরচ হল:(50*1) + (34 * 2) + (8 * 3) =142 (ন্যূনতম)

অ্যালগরিদম

optCostBst(keys, freq, n)
Input: Keys to insert in BST, frequency for each keys, number of keys.
Output: Minimum cost to make optimal BST.
Begin
   define cost matrix of size n x n
   for i in range 0 to n-1, do
      cost[i, i] := freq[i]
   done
   for length in range 2 to n, do
      for i in range 0 to (n-length+1), do
         j := i + length – 1
         cost[i, j] := ∞
         for r in range i to j, done
            if r > i, then
               c := cost[i, r-1]
            else
               c := 0
            if r < j, then
               c := c + cost[r+1, j]
            c := c + sum of frequency from i to j
            if c < cost[i, j], then
               cost[i, j] := c
         done
      done
   done
   return cost[0, n-1]
End

উদাহরণ

#include <iostream>
using namespace std;
int sum(int freq[], int low, int high){ //sum of frequency from low to high range
   int sum = 0;
   for (int k = low; k <=high; k++)
      sum += freq[k];
   return sum;
}
int minCostBST(int keys[], int freq[], int n){
   int cost[n][n];
   for (int i = 0; i < n; i++) //when only one key, move along diagonal elements
      cost[i][i] = freq[i];
   for (int length=2; length<=n; length++){
      for (int i=0; i<=n-length+1; i++){ //from 0th row to n-length+1 row as i
         int j = i+length-1;
         cost[i][j] = INT_MAX; //initially store to infinity
         for (int r=i; r<=j; r++){
            //find cost when r is root of subtree
            int c = ((r > i)?cost[i][r-1]:0)+((r < j)?cost[r+1][j]:0)+sum(freq, i, j);
            if (c < cost[i][j])
               cost[i][j] = c;
         }
      }
   }
   return cost[0][n-1];
}
int main(){
   int keys[] = {10, 12, 20};
   int freq[] = {34, 8, 50};
   int n = 3;
   cout << "Cost of Optimal BST is: "<< minCostBST(keys, freq, n);
}

আউটপুট

Cost of Optimal BST is: 142