একটি সিমেট্রিক মিন-ম্যাক্স হিপ (SMMH) একটি সম্পূর্ণ বাইনারি ট্রি হিসাবে সংজ্ঞায়িত করা হয় যেখানে রুট ছাড়া প্রতিটি নোডে ঠিক একটি উপাদান থাকে। একটি SMMH এর মূলটি খালি থাকবে এবং SMMH-এ মোট নোডের সংখ্যা হল m + 1, যেখানে m হল উপাদানগুলির সংখ্যা৷
y SMMH এর যেকোনো নোড হতে দিন। এলিমেন্ট(y) কে y তে রুট করা সাব ট্রির উপাদান হতে দিন কিন্তু y তে উপাদান (যদি থাকে) বাদ দিয়ে। অনুমান করুন যে উপাদানগুলি(y) j =∅। y নিম্নলিখিত বৈশিষ্ট্যগুলিকে সন্তুষ্ট করে:
- y এর বাম সন্তানের উপাদান(y) এ ন্যূনতম উপাদান রয়েছে।
- y এর ডান সন্তানের (যদি থাকে) উপাদানে (y) সর্বোচ্চ উপাদান রয়েছে।
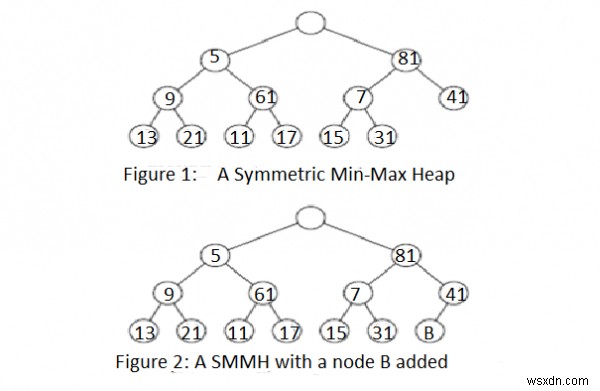
চিত্র 1 একটি SMMH উদাহরণ দেখায় যাতে 12টি উপাদান রয়েছে৷
যখন y নোডকে 81 দিয়ে বোঝায়, উপাদান(y) ={7, 15, 31, 41}; y এর বাম সন্তানের উপাদান(y) এ ন্যূনতম উপাদান 6 আছে; এবং y এর ডান সন্তানের উপাদান(y) এ সর্বোচ্চ 41টি উপাদান রয়েছে। আমরা যাচাই করতে পারি যে এই SMMH-এর প্রতিটি নোড y উল্লেখিত বৈশিষ্ট্যগুলিকে সন্তুষ্ট করে৷
যেহেতু একটি SMMH একটি সম্পূর্ণ বাইনারি ট্রি হিসাবে চিহ্নিত করা হয়, এটি একটি সম্পূর্ণ বাইনারি গাছের মান ম্যাপিংকে একটি অ্যারেতে বাস্তবায়ন করে একটি অন্তর্নিহিত ডেটা কাঠামো হিসাবে সংরক্ষণ করা হয়। যখন m =1 হয়, ন্যূনতম এবং সর্বোচ্চ উপাদানগুলি একই থাকে এবং SMMH এর মূলের বাম দিকের চাইল্ডে থাকে৷
যখন m> 1, সর্বনিম্ন উপাদানটি মূলের বাম সন্তানে এবং সর্বাধিক উপাদানটি মূলের ডান শিশুটিতে থাকে। সুতরাং getMin এবং getMax অপারেশনগুলি O(1) সময় ব্যয় করে।
এটা দেখা সহজ যে একটি m + 1-নোড সম্পূর্ণ বাইনারি ট্রি একটি খালি রুট সহ এবং প্রতিটি অন্য নোডে একটি উপাদান একটি SMMH যদি নিম্নলিখিতগুলি সত্য হয় -
A1 − প্রতিটি নোড y এর জন্য যার একটি ডান ভাইবোন আছে, y এর উপাদানটি y এর ডান ভাইবোনের থেকে কম বা সমান৷
A2 − দাদা-দাদি আছে এমন প্রতিটি নোড y-এর জন্য, দাদা-দাদির বাম সন্তানের উপাদানটি y-এর থেকে কম বা সমান।
A3 − দাদা-দাদি আছে এমন প্রতিটি নোড y-এর জন্য, দাদা-দাদির ডান সন্তানের উপাদানটি y-এর থেকে বড় বা সমান।
লক্ষ্য করুন যে যদি সম্পত্তি A1 নোড y-এ সন্তুষ্ট হয়, তাহলে A2 এবং A3-এর মধ্যে সর্বাধিক একটি y-তে লঙ্ঘন হতে পারে। বৈশিষ্ট্যগুলি A1 থেকে A3 প্রয়োগ করে আমরা উপাদানগুলি সন্নিবেশ করা এবং অপসারণ করতে সহজ অ্যালগরিদমগুলিতে পৌঁছাই। এই অ্যালগরিদমগুলি হল ন্যূনতম এবং সর্বোচ্চ হিপের জন্য সংশ্লিষ্ট অ্যালগরিদমের সহজ অভিযোজন৷ তাদের জটিলতা হল O(log m)।
এখানে, আমরা সন্নিবেশ অপারেশন নির্দিষ্ট. ধরুন আমরা চিত্র 1-এর SMMH-এ 3 সন্নিবেশ করতে চাই। যেহেতু একটি SMMH একটি সম্পূর্ণ বাইনারি ট্রি, তাই চিত্র 2-এ দেখানো অবস্থানে আমাদের অবশ্যই SMMH-এ একটি নতুন নোড যোগ করতে হবে; নতুন নোডকে B.
হিসেবে লেবেল করা হয়েছেআমাদের উদাহরণে, B একটি খালি নোড নির্দেশ করবে। এখন 3 নোড B এ ঢোকানো হয়েছে।


