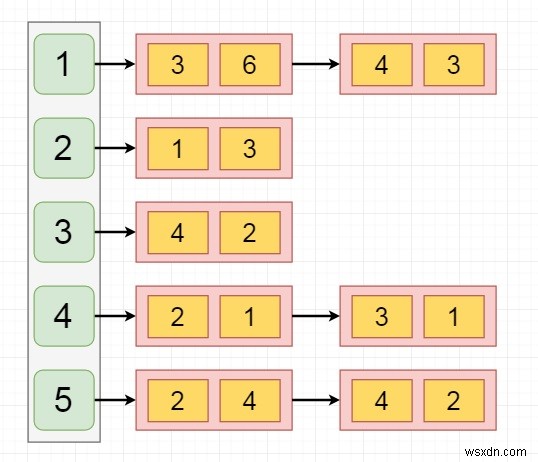
যেমন আমরা জানি যে গ্রাফগুলিকে বিভিন্ন বৈচিত্রের মধ্যে শ্রেণীবদ্ধ করা যেতে পারে৷ তারা নির্দেশিত বা অনির্দেশিত হতে পারে, এবং তারা ওজনযুক্ত বা ওজনহীন হতে পারে। এখানে আমরা দেখব কিভাবে মেমরিতে ওজনযুক্ত গ্রাফ উপস্থাপন করা যায়। নিচের গ্রাফটি বিবেচনা করুন −
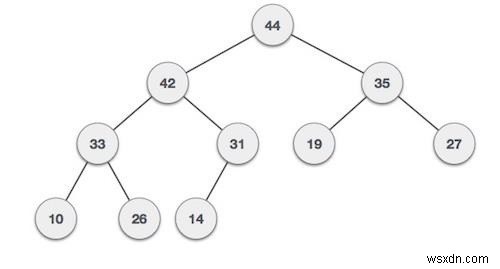
সংলগ্ন ম্যাট্রিক্স উপস্থাপনা
সংলগ্ন ম্যাট্রিক্স ফর্ম ব্যবহার করে ওজনযুক্ত গ্রাফ সঞ্চয় করতে, আমরা ম্যাট্রিক্সকে খরচ ম্যাট্রিক্স বলে থাকি। এখানে M[i, j] অবস্থানে থাকা প্রতিটি কোষ প্রান্ত i থেকে j পর্যন্ত ওজন ধরে রেখেছে। যদি প্রান্তটি উপস্থিত না থাকে তবে এটি অসীম হবে। একই নোডের জন্য, এটি 0 হবে।
| 0 | ∞ | 6 | 3 | ∞ |
| 3 | 0 | ∞ | ∞ | ∞ |
| ∞ | ∞ | 0 | 2 | ∞ |
| ∞ | 1 | ৷1 | ৷0 | ∞ |
| ∞ | 4 | ৷∞ | 2 | 0 |
সংলগ্ন তালিকা প্রতিনিধিত্ব
সংলগ্ন তালিকায়, তালিকার প্রতিটি উপাদানের দুটি মান থাকবে। প্রথমটি গন্তব্য নোড, এবং দ্বিতীয়টি এই দুটি নোডের মধ্যে ওজন। উপস্থাপনাটি নিচের মত।