সময়ের জটিলতা হল সবচেয়ে আকর্ষণীয় ধারণাগুলির মধ্যে একটি যা আপনি কম্পিউটার বিজ্ঞান থেকে শিখতে পারেন এবং এটি বুঝতে আপনার কোনো ডিগ্রির প্রয়োজন নেই!
এটি আকর্ষণীয় কারণ এটি আপনাকে দেখতে সাহায্য করে কেন একটি নির্দিষ্ট অ্যালগরিদম বা প্রোগ্রাম ধীর হতে পারে এবং আপনি এটি দ্রুত করতে কি করতে পারেন।
আপনি এটি আপনার নিজের কোডে প্রয়োগ করতে পারেন৷
৷এটি সব অভিনব অ্যালগরিদম ছাড়িয়ে যায়৷ যা আপনি কম্পিউটার বিজ্ঞানের বইয়ে পাবেন, যেমনটি আমি এই নিবন্ধে পরে আপনার জন্য প্রদর্শন করব।
কিন্তু প্রথমে আমাদের কথা বলা দরকার কোনটা ধীর আর কোনটা দ্রুত।
ধীর বনাম দ্রুত
150ms (মিলিসেকেন্ড) মধ্যে 1 মিলিয়ন সংখ্যা বাছাই কি ধীর বা দ্রুত?
আমি মনে করি এটি বেশ দ্রুত, কিন্তু এটি এমন প্রশ্ন নয় যে সময় জটিলতা উত্তর দেওয়ার চেষ্টা করছে৷
৷আমরা জানতে চাই কিভাবে একটি অ্যালগরিদম "ইনপুট সাইজ" বাড়ার সাথে সাথে কাজ করবে।
যখন আমরা "ইনপুট আকার" সম্পর্কে কথা বলি তখন আমরা ফাংশন বা পদ্ধতির আর্গুমেন্ট সম্পর্কে কথা বলি। যদি একটি পদ্ধতি একটি আর্গুমেন্ট হিসাবে একটি স্ট্রিং নেয় তাহলে সেটি হল ইনপুট, এবং স্ট্রিং এর দৈর্ঘ্য হল ইনপুট সাইজ৷
বিগ ও নোটেশন
Big O স্বরলিপির সাহায্যে আমরা অ্যালগরিদমকে তাদের কর্মক্ষমতা অনুযায়ী শ্রেণীবদ্ধ করতে পারি।
এটা এই মত দেখায়:
O(1)
এই ক্ষেত্রে O(1) একটি "স্থির সময়" অ্যালগরিদম প্রতিনিধিত্ব করে৷
এর মানে হল যে অ্যালগরিদম সবসময় তার কাজ শেষ করতে একই সময় নেয়, তা নির্বিশেষে এটি যত কাজই করুক না কেন।
আরেকটি হল "রৈখিক সময়":
O(n)
যেখানে "n" ইনপুটের আকার (স্ট্রিং আকার, অ্যারের আকার, ইত্যাদি) উপস্থাপন করে। এর মানে হল যে অ্যালগরিদম তার কাজটি ইনপুট আকারের সাথে 1:1 এর মধ্যে শেষ করবে, তাই ইনপুট আকার দ্বিগুণ করলে কাজটি সম্পূর্ণ করতে যে সময় লাগে তার দ্বিগুণ হবে৷
এখানে একটি টেবিল আছে :
| নোটেশন | নাম | বর্ণনা |
|---|---|---|
| O(1) | ধ্রুবক | সর্বদা একই সময় নেয়৷ | ৷
| O(log n) | লগারিদমিক | প্রতিটি লুপ পুনরাবৃত্তির পরে কাজের পরিমাণকে 2 দ্বারা ভাগ করা হয় (বাইনারী অনুসন্ধান)। |
| O(n) | রৈখিক | কাজ সম্পূর্ণ করার সময় ইনপুট আকারের সাথে 1 থেকে 1 বৃদ্ধি পায়৷ |
| O(n log n) | রৈখিক | এটি একটি নেস্টেড লুপ, যেখানে ভিতরের লুপ log n এ চলে সময় উদাহরণগুলির মধ্যে রয়েছে quicksort, mergesort &heapsort. |
| O(n^2) | চতুর্মুখী | কাজ সম্পূর্ণ করার সময় input size ^ 2 এ বাড়ে সম্পর্ক আপনি এটি চিনতে পারেন যখনই আপনার কাছে একটি লুপ থাকে যা সমস্ত উপাদানের উপর যায় এবং লুপের প্রতিটি পুনরাবৃত্তিও প্রতিটি উপাদানের উপর যায়। আপনার একটি নেস্টেড লুপ আছে৷ | ৷
| O(n^3) | কিউবিক | n^2 এর মতই , কিন্তু সময় একটি n^3 এ বৃদ্ধি পায় ইনপুট আকারের সাথে সম্পর্ক। এটিকে চিনতে একটি ট্রিপল নেস্টেড লুপ খুঁজুন৷ | ৷
| O(2^n) | Exponential | কাজ সম্পূর্ণ করার সময় 2 ^ input size বাড়ে সম্পর্ক এটি n^2 এর চেয়ে অনেক ধীর , তাই তাদের বিভ্রান্ত করবেন না! একটি উদাহরণ হল পুনরাবৃত্ত ফিবোনাচি অ্যালগরিদম৷ | ৷
অ্যালগরিদম বিশ্লেষণ
আপনি যদি "n" উপাদানগুলির একটি অ্যারে হিসাবে ইনপুট সম্পর্কে চিন্তা করেন তবে আপনি এর জন্য আপনার অন্তর্দৃষ্টি বিকাশ শুরু করতে পারেন৷
কল্পনা করুন যে আপনি জোড় সংখ্যার সমস্ত উপাদান খুঁজে পেতে চান, এটি করার একমাত্র উপায় হল প্রতিটি উপাদান একবার পড়ে দেখুন যে এটি শর্তের সাথে মেলে কিনা।
[1,2,3,4,5,6,7,8,9,10].select(&:even?)
আপনি নম্বরগুলি এড়িয়ে যেতে পারবেন না কারণ আপনি যে নম্বরগুলি খুঁজছেন তার কিছু মিস করতে পারেন, যাতে এটি একটি লিনিয়ার টাইম অ্যালগরিদম O(n) .
একই সমস্যার ৩টি ভিন্ন সমাধান
পৃথক উদাহরণ বিশ্লেষণ করা আকর্ষণীয়, কিন্তু এই ধারণাটি বুঝতে সাহায্য করে যেটি আমরা বিভিন্ন সমাধান ব্যবহার করে কীভাবে একই সমস্যা সমাধান করতে পারি তা দেখা।
আমরা একটি স্ক্র্যাবল সমাধান চেকারের জন্য 3টি কোড উদাহরণ অন্বেষণ করতে যাচ্ছি।
স্ক্র্যাবল এমন একটি গেম যা অক্ষরের একটি তালিকা দেয় (যেমন ollhe ) আপনাকে শব্দ গঠন করতে বলে (যেমন hello ) এই অক্ষরগুলি ব্যবহার করে৷
এখানে প্রথম সমাধান :
def scramble(অক্ষর, শব্দ) word.each_char.all? { |c| characters.count(c)>=word.count(c) }শেষ
আপনি কি জানেন এই কোডের সময় জটিলতা কি? কীটি count-এ রয়েছে পদ্ধতি, তাই নিশ্চিত করুন যে আপনি বুঝতে পেরেছেন যে পদ্ধতিটি কী করে৷
উত্তর হল:O(n^2) .
এবং এর কারণ হল each_char এর সাথে আমরা word স্ট্রিং-এর সমস্ত অক্ষর ধরে যাচ্ছি . এটি একাই একটি লিনিয়ার টাইম অ্যালগরিদম হবে O(n) , কিন্তু ব্লকের ভিতরে আমাদের count আছে পদ্ধতি।
এই পদ্ধতিটি কার্যকরীভাবে আরেকটি লুপ যা স্ট্রিংয়ের সমস্ত অক্ষরকে আবার গণনা করার জন্য যায়।
দ্বিতীয় সমাধান
ঠিক আছে।
আমরা কিভাবে ভাল করতে পারি? আমাদের কিছু লুপিং বাঁচানোর একটি উপায় আছে?
অক্ষর গণনা করার পরিবর্তে আমরা সেগুলি সরিয়ে ফেলতে পারি, এইভাবে আমাদের কাছে কম অক্ষর আছে।
এখানে দ্বিতীয় সমাধান :
def scramble(অক্ষর, শব্দ) অক্ষর =characters.dup word.each_char.all? { |c| characters.sub!(c, "") }শেষ
এই এক একটু বেশি আকর্ষণীয়. এটি count থেকে অনেক দ্রুত হবে সর্বোত্তম ক্ষেত্রে সংস্করণ, যেখানে আমরা যে অক্ষরগুলি খুঁজছি তা স্ট্রিংয়ের শুরুর কাছাকাছি।
কিন্তু যখন অক্ষরগুলো সব শেষে থাকে, তখন word-এ সেগুলো কীভাবে পাওয়া যায় তার বিপরীত ক্রমে , কর্মক্ষমতা count এর মতই হবে সংস্করণ, তাই আমরা বলতে পারি যে এটি এখনও একটি O(n^2) অ্যালগরিদম।
আমাদের সেই ক্ষেত্রে চিন্তা করতে হবে না যেখানে word-এর কোনো অক্ষর নেই উপলব্ধ, কারণ all? sub! এর সাথে সাথেই পদ্ধতি বন্ধ হয়ে যাবে false ফেরত দেয় . তবে আপনি এটি তখনই জানতে পারবেন যদি আপনি রুবি সম্পর্কে বিস্তৃতভাবে অধ্যয়ন করেন, যা আপনাকে নিয়মিত রুবি কোর্সগুলি অফার করে তার বাইরে৷
আসুন অন্য পদ্ধতির সাথে চেষ্টা করি
যদি আমরা ব্লকের ভিতরে কোন ধরনের লুপিং সরিয়ে ফেলি? আমরা এটি একটি হ্যাশ দিয়ে করতে পারি।
def scramble(অক্ষর, শব্দ) উপলব্ধ =Hash.new(1) characters.each_char { |c| উপলব্ধ[c] +=1 } word.each_char.all? { |c| উপলব্ধ [c] -=1; উপলব্ধ [c]> 0 }শেষ
হ্যাশ মান পড়া এবং লেখা একটি O(1) অপারেশন, যার মানে এটি বেশ দ্রুত, বিশেষ করে লুপিংয়ের তুলনায়।
আমাদের এখনও দুটি লুপ আছে :
একটি হ্যাশ টেবিল নির্মাণ, এবং এক এটি চেক. কারণ এই লুপগুলি নেস্ট করা নেই এটি একটি O(n) অ্যালগরিদম।
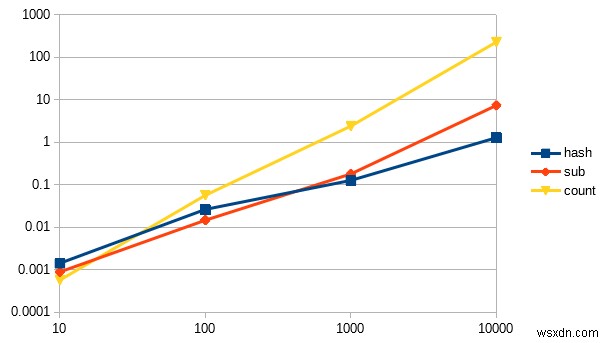
যদি আমরা এই 3টি সমাধানকে বেঞ্চমার্ক করি তাহলে আমরা দেখতে পাব যে আমাদের বিশ্লেষণ ফলাফলের সাথে মিলে যায়:
হ্যাশ 1.216667 0.000000 1.216667 ( 1.216007) সাব 6.240000 1.023333 7.263333 (7.268173) গণনা 222.8666473 (222.8666473) প্রি 222.8666437 এখানে একটি লাইন চার্ট:
কিছু জিনিস লক্ষ্য করুন :
- ওয়াই অক্ষ (উল্লম্ব) নির্দেশ করে যে কাজটি সম্পূর্ণ করতে কত সেকেন্ড লেগেছিল, যখন X অক্ষ (অনুভূমিক) ইনপুট আকারকে উপস্থাপন করে৷
- এটি একটি লগারিদমিক চার্ট, যা একটি নির্দিষ্ট পরিসরে মানগুলিকে সংকুচিত করে, কিন্তু বাস্তবে
countলাইন অনেক খাড়া।- আমি এটিকে লগারিদমিক চার্ট তৈরি করার কারণ হল আপনি একটি আকর্ষণীয় প্রভাবের প্রশংসা করতে পারেন, একটি খুব ছোট ইনপুট আকার
countআসলে দ্রুত!সারাংশ
আপনি অ্যালগরিদমিক সময় জটিলতা, বড় ও স্বরলিপি এবং সময় জটিলতা বিশ্লেষণ সম্পর্কে শিখেছেন। আপনি কয়েকটি উদাহরণও দেখেছেন যেখানে আমরা একই সমস্যার বিভিন্ন সমাধান তুলনা করেছি এবং তাদের কর্মক্ষমতা বিশ্লেষণ করেছি।
আশা করি আপনি নতুন এবং আকর্ষণীয় কিছু শিখেছেন!
আপনি যদি এই পোস্টটি সোশ্যাল মিডিয়াতে শেয়ার করেন এবং নিউজলেটারে সাবস্ক্রাইব করুন যদি আপনি এখনও না করে থাকেন তাহলে আমি আপনাকে এই ধরনের আরও সামগ্রী পাঠাতে পারি৷
পড়ার জন্য ধন্যবাদ।